Statistics From 10^5 Meters - Introduction

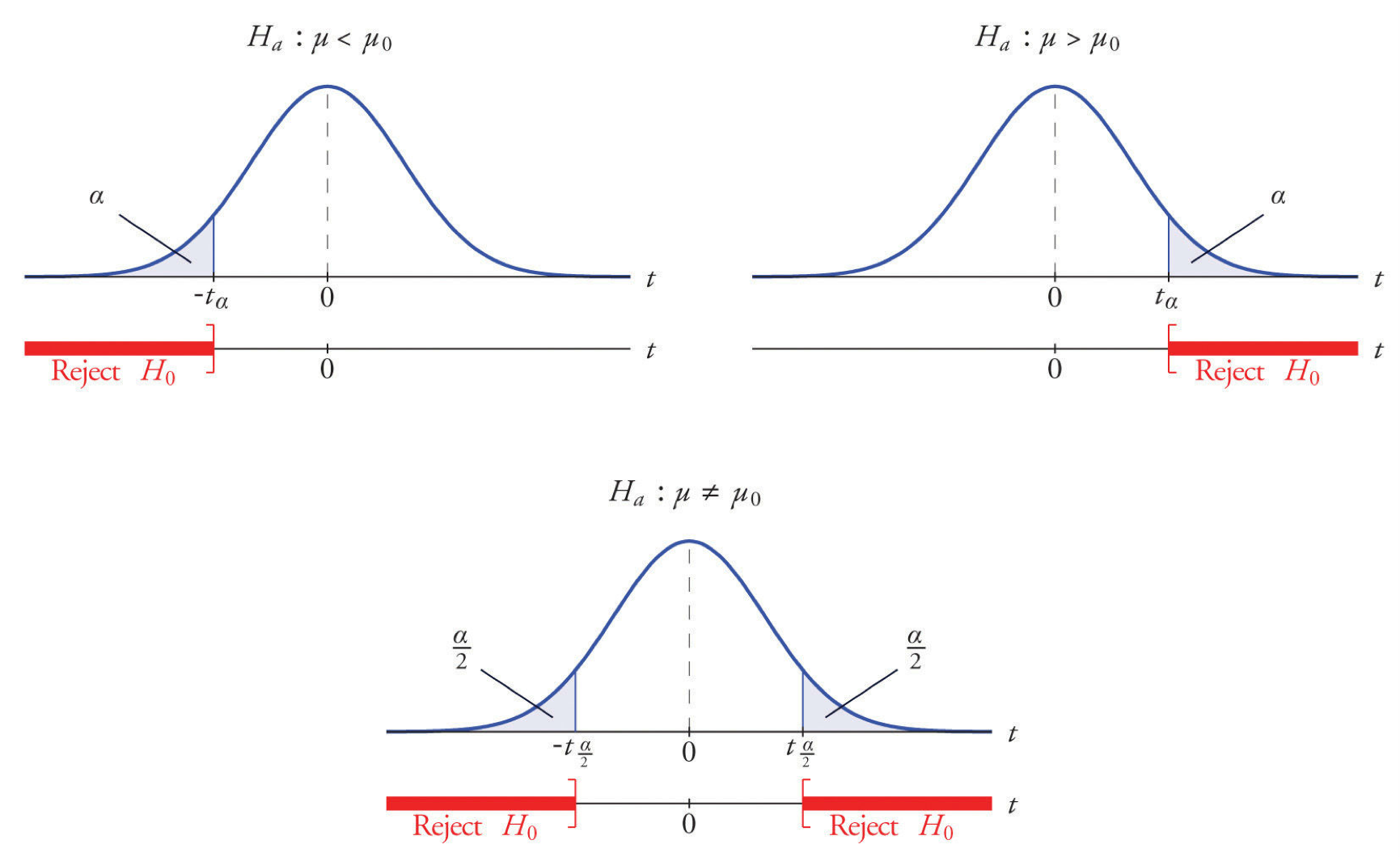Rejection regions in hypothesis testing.

De-jargonizing and desmystifying.

Statistics jargon can be confusing, especially for newcomers. Many terms are related and represent overlapping (and sometimes fuzzy) concepts. They can be used interchangeably and loosely as a shorthand. This isn’t usually an issue once you’ve internalized these concepts but for those new to the field it can be a source of some frustration at first.

Statistics isn’t terribly special here, I think it’s the same with any jargon, though the underlying mathematical language in which statistics is framed may make its jargon a bit more problematic, frustrating, or intimidating for some.

Those well-versed in probability or statistics can speak loosely about a “distribution” or switch between “inference” and “estimation” with little risk of miscommunication or misunderstanding. But the new student doesn’t have the familiarity to feel comfortable with this looseness, and concepts and terms can get muddled when they’re used in a casual and imprecise way.

This was definitely my experience when I began learning statistics. I remember authors throwing the word “model” around like hippies throw around the word “energy”. Granted, at the time I was recovering mathematician, so my needs for precise definitions were borderline unhealthy, but I’m going out on limb based on years of tutoring stats and say lots of folks have had similar experiences.

The intent of this series is to clarify concepts and terms from probability and statistics and thus, to some extent de-jargonize the jargon. We’ll stay very high level and won’t dive too deeply into any one topic. We’ll only linger long enough to develop an understanding sufficient to identify and clarify the distinctions between concepts.

Mostly we’ll be doing some compare and contrast, with liberal use of examples. I’ll try to include concrete code and visualizations to give some grounding to the abstractions.

In my experience, most humans learn by moving from the concrete and specific to the abstract and general. We are very good at seeing several examples and detecting a pattern – it’s much rarer in my experience to move the other direction. Furthermore, we sharpen our conceptual understanding by seeing how concepts are the same and how they differ, which takes a bit of time and attention.

The exposition I’ve seen in some mathematical and statistical classes, textbooks and references doesn’t seem to reflect this - perhaps it’s cultural or maybe those attracted to the field are skilled at the general -> specific learning paradigm.

Hopefully the de-jargonizing we do in this series will also be de-mystifying. This process is in my humble opinion necessary but not sufficient for deeper understanding and a natural first, or at least early, step.

Some clarification can of course only come in pursuit of said deeper understanding, but we’ll do our best to help shortcut that process.