Ames Housing Data Processing, analysis and predictive modeling
Exploratory analysis
In a previous notebook, we processed and cleaned the Ames housing dataset. In this notebook, we focus on exploring the variables and the relationships among them. In a later notebook we’ll model and predict sale prices.
Contents
Setup
# standard imports
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
import scipy.stats as ss
import sys
import os
# add parent directory for importing custom classes
pardir = os.path.abspath(os.path.join(os.getcwd(), os.pardir))
sys.path.append(pardir)
# add root site-packages directory to workaround pyitlib pip install issue
sys.path.append('/Users/home/anaconda3/lib/python3.7/site-packages')
# custom classes
from codes.process import DataDescription
from codes.explore import *
# notebook settings
warnings.filterwarnings('ignore')
plt.style.use('seaborn-white')
sns.set_style('white')
Load and inspect data
data_dir = '../data'
file_names = ['orig.csv', 'clean.csv']
hp_data = load_datasets(data_dir, file_names)
orig, clean = (hp_data.dfs['orig'], hp_data.dfs['clean'])
We have 2 versions of the dataset here (created in a previous notebook)
origis the original dataset with no preprocessingcleanis the preprocessed dataset, with problematic variables and observations dropped and missing values imputed
. In this notebook we’ll primarily be working with the cleaned dataset
clean.data.head()
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | LotShape | LandContour | Utilities | LotConfig | LandSlope | ... | ScreenPorch | PoolArea | PoolQC | Fence | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | ||||||||||||||||||||||
| train | 1 | 60 | RL | 65.0 | 8450.0 | Pave | 0 | Lvl | 3 | Inside | 0 | ... | 0.0 | 0.0 | 0 | 0 | 0.0 | 2 | 2008 | WD | Normal | 208500.0 |
| 2 | 20 | RL | 80.0 | 9600.0 | Pave | 0 | Lvl | 3 | FR2 | 0 | ... | 0.0 | 0.0 | 0 | 0 | 0.0 | 5 | 2007 | WD | Normal | 181500.0 | |
| 3 | 60 | RL | 68.0 | 11250.0 | Pave | 1 | Lvl | 3 | Inside | 0 | ... | 0.0 | 0.0 | 0 | 0 | 0.0 | 9 | 2008 | WD | Normal | 223500.0 | |
| 4 | 70 | RL | 60.0 | 9550.0 | Pave | 1 | Lvl | 3 | Corner | 0 | ... | 0.0 | 0.0 | 0 | 0 | 0.0 | 2 | 2006 | WD | Abnorml | 140000.0 | |
| 5 | 60 | RL | 84.0 | 14260.0 | Pave | 1 | Lvl | 3 | FR2 | 0 | ... | 0.0 | 0.0 | 0 | 0 | 0.0 | 12 | 2008 | WD | Normal | 250000.0 |
5 rows × 78 columns
clean.data.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 2916 entries, (train, 1) to (test, 2919)
Data columns (total 78 columns):
MSSubClass 2916 non-null category
MSZoning 2916 non-null category
LotFrontage 2916 non-null float64
LotArea 2916 non-null float64
Street 2916 non-null category
LotShape 2916 non-null int64
LandContour 2916 non-null category
Utilities 2916 non-null int64
LotConfig 2916 non-null category
LandSlope 2916 non-null int64
Neighborhood 2916 non-null category
Condition1 2916 non-null category
Condition2 2916 non-null category
BldgType 2916 non-null category
HouseStyle 2916 non-null category
OverallQual 2916 non-null int64
OverallCond 2916 non-null int64
YearBuilt 2916 non-null float64
YearRemodAdd 2916 non-null float64
RoofStyle 2916 non-null category
RoofMatl 2916 non-null category
Exterior1st 2916 non-null category
Exterior2nd 2916 non-null category
MasVnrType 2916 non-null category
MasVnrArea 2916 non-null float64
ExterQual 2916 non-null int64
ExterCond 2916 non-null int64
Foundation 2916 non-null category
BsmtQual 2916 non-null int64
BsmtCond 2916 non-null int64
BsmtExposure 2916 non-null int64
BsmtFinType1 2916 non-null int64
BsmtFinSF1 2916 non-null float64
BsmtFinType2 2916 non-null int64
BsmtFinSF2 2916 non-null float64
BsmtUnfSF 2916 non-null float64
TotalBsmtSF 2916 non-null float64
Heating 2916 non-null category
HeatingQC 2916 non-null int64
CentralAir 2916 non-null category
Electrical 2916 non-null category
1stFlrSF 2916 non-null float64
2ndFlrSF 2916 non-null float64
LowQualFinSF 2916 non-null float64
GrLivArea 2916 non-null float64
BsmtFullBath 2916 non-null int64
BsmtHalfBath 2916 non-null int64
FullBath 2916 non-null int64
HalfBath 2916 non-null int64
BedroomAbvGr 2916 non-null int64
KitchenAbvGr 2916 non-null int64
KitchenQual 2916 non-null int64
TotRmsAbvGrd 2916 non-null int64
Functional 2916 non-null int64
Fireplaces 2916 non-null int64
FireplaceQu 2916 non-null int64
GarageType 2916 non-null category
GarageYrBlt 2916 non-null float64
GarageFinish 2916 non-null int64
GarageCars 2916 non-null int64
GarageArea 2916 non-null float64
GarageQual 2916 non-null int64
GarageCond 2916 non-null int64
PavedDrive 2916 non-null int64
WoodDeckSF 2916 non-null float64
OpenPorchSF 2916 non-null float64
EnclosedPorch 2916 non-null float64
3SsnPorch 2916 non-null float64
ScreenPorch 2916 non-null float64
PoolArea 2916 non-null float64
PoolQC 2916 non-null int64
Fence 2916 non-null int64
MiscVal 2916 non-null float64
MoSold 2916 non-null int64
YrSold 2916 non-null int64
SaleType 2916 non-null category
SaleCondition 2916 non-null category
SalePrice 1457 non-null float64
dtypes: category(22), float64(23), int64(33)
memory usage: 1.3+ MB
The response variable SalePrice
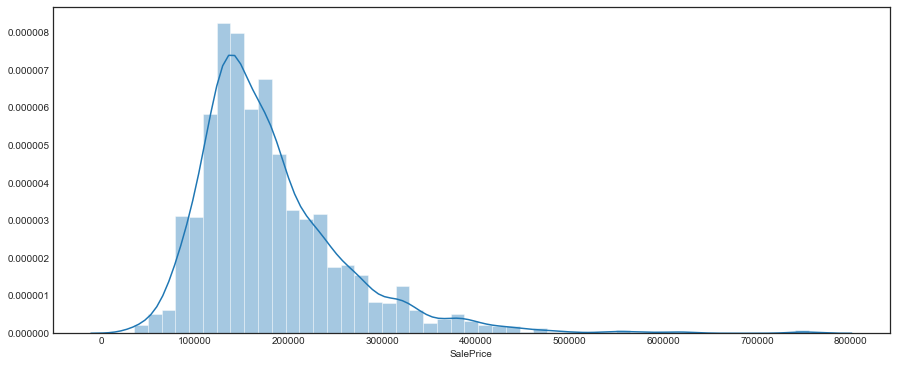
First let’s look at the distribution of SalePrice, the variable we’ll later be interested in predicting.
sale_price = clean.data.loc['train', :]['SalePrice']
plt.figure(figsize=(15, 6))
sns.distplot(sale_price)
<matplotlib.axes._subplots.AxesSubplot at 0x11c407cc0>
plt.figure(figsize=(15, 6))
sns.swarmplot(sale_price)
<matplotlib.axes._subplots.AxesSubplot at 0x11c580d68>
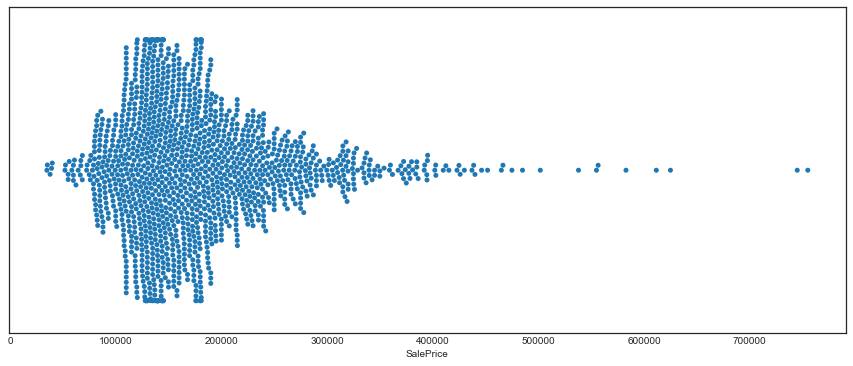
The distribution is positively skewed, with a long right tail. There are two observations with SalePrice > 700000, and with a good separation from the rest of the points.
# check skewness of SalePrice
sale_price.skew()
1.88374941136315
Testing log-normality
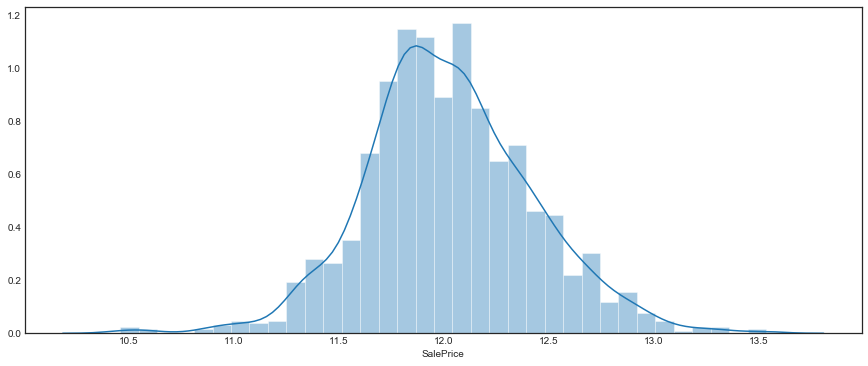
The distribution looks like it may be approximately log-normal, let’s check this
# distribution of log(SalePrice)
plt.figure(figsize=(15, 6))
sns.distplot(np.log(sale_price))
<matplotlib.axes._subplots.AxesSubplot at 0x11c733b00>
QQ-plot
# lognormal QQ plot
plt.figure(figsize=(8, 8))
# standard deviation of log is the shape parameter
s = np.log(sale_price).std()
lognorm = ss.lognorm(s)
ss.probplot(sale_price, dist=lognorm, plot=plt)
plt.show()
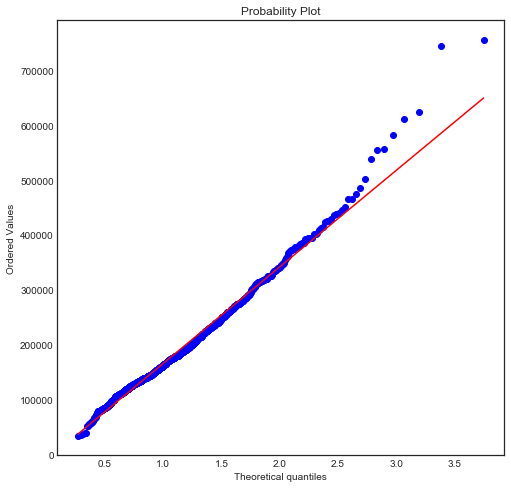
The distribution appears to be approxiately log-normal, although the QQ plot shows the right tail is a bit longer than expected, and the two observations with highest SalePrice are much higher than expected.
Kolmogorov - Smirnov test
This is a non-parametric test for comparing distributions. We’ll use scipy.stats implementation
ss.kstest(sale_price, lognorm.cdf)
KstestResult(statistic=1.0, pvalue=0.0)
This test conclusively rejects the null hypothesis that the distribution of SalePrice is lognormal. Nevertheless, the plots indicate that log-normality is perhaps a usefull approximation. Moreover, log(SalePrice) may be more useful than SalePrice for prediction purposes, given the symmetry of its distribution.
Categorical variables
First we look at all categorical variables, that is, all discrete variables with no ordering on the values. In our cleaned dataframe these are all the columns with category dtype
# dataframe of categorical variables
cats = HPDataFramePlus(data=clean.data.select_dtypes('category'))
cats.data.head()
| MSSubClass | MSZoning | Street | LandContour | LotConfig | Neighborhood | Condition1 | Condition2 | BldgType | HouseStyle | ... | Exterior1st | Exterior2nd | MasVnrType | Foundation | Heating | CentralAir | Electrical | GarageType | SaleType | SaleCondition | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | ||||||||||||||||||||||
| train | 1 | 60 | RL | Pave | Lvl | Inside | CollgCr | Norm | Norm | 1Fam | 2Story | ... | VinylSd | VinylSd | BrkFace | PConc | GasA | Y | SBrkr | Attchd | WD | Normal |
| 2 | 20 | RL | Pave | Lvl | FR2 | Veenker | Feedr | Norm | 1Fam | 1Story | ... | MetalSd | MetalSd | None | CBlock | GasA | Y | SBrkr | Attchd | WD | Normal | |
| 3 | 60 | RL | Pave | Lvl | Inside | CollgCr | Norm | Norm | 1Fam | 2Story | ... | VinylSd | VinylSd | BrkFace | PConc | GasA | Y | SBrkr | Attchd | WD | Normal | |
| 4 | 70 | RL | Pave | Lvl | Corner | Crawfor | Norm | Norm | 1Fam | 2Story | ... | Wd Sdng | Wd Shng | None | BrkTil | GasA | Y | SBrkr | Detchd | WD | Abnorml | |
| 5 | 60 | RL | Pave | Lvl | FR2 | NoRidge | Norm | Norm | 1Fam | 2Story | ... | VinylSd | VinylSd | BrkFace | PConc | GasA | Y | SBrkr | Attchd | WD | Normal |
5 rows × 22 columns
# print description of categorical variables
desc = DataDescription('../data/data_description.txt')
cats.desc = desc
cats.print_desc(cols=cats.data.columns)
MSSubClass: Identifies the type of dwelling involved in the sale.
20 - 1-STORY 1946 & NEWER ALL STYLES
30 - 1-STORY 1945 & OLDER
40 - 1-STORY W/FINISHED ATTIC ALL AGES
45 - 1-1/2 STORY - UNFINISHED ALL AGES
50 - 1-1/2 STORY FINISHED ALL AGES
60 - 2-STORY 1946 & NEWER
70 - 2-STORY 1945 & OLDER
75 - 2-1/2 STORY ALL AGES
80 - SPLIT OR MULTI-LEVEL
85 - SPLIT FOYER
90 - DUPLEX - ALL STYLES AND AGES
120 - 1-STORY PUD (Planned Unit Development) - 1946 & NEWER
150 - 1-1/2 STORY PUD - ALL AGES
160 - 2-STORY PUD - 1946 & NEWER
180 - PUD - MULTILEVEL - INCL SPLIT LEV/FOYER
190 - 2 FAMILY CONVERSION - ALL STYLES AND AGES
MSZoning: Identifies the general zoning classification of the sale.
A - Agriculture
C - Commercial
FV - Floating Village Residential
I - Industrial
RH - Residential High Density
RL - Residential Low Density
RP - Residential Low Density Park
RM - Residential Medium Density
Street: Type of road access to property
Grvl - Gravel
Pave - Paved
LandContour: Flatness of the property
Lvl - Near Flat/Level
Bnk - Banked - Quick and significant rise from street grade to building
HLS - Hillside - Significant slope from side to side
Low - Depression
LotConfig: Lot configuration
Inside - Inside lot
Corner - Corner lot
CulDSac - Cul-de-sac
FR2 - Frontage on 2 sides of property
FR3 - Frontage on 3 sides of property
Neighborhood: Physical locations within Ames city limits
Blmngtn - Bloomington Heights
Blueste - Bluestem
BrDale - Briardale
BrkSide - Brookside
ClearCr - Clear Creek
CollgCr - College Creek
Crawfor - Crawford
Edwards - Edwards
Gilbert - Gilbert
IDOTRR - Iowa DOT and Rail Road
MeadowV - Meadow Village
Mitchel - Mitchell
Names - North Ames
NoRidge - Northridge
NPkVill - Northpark Villa
NridgHt - Northridge Heights
NWAmes - Northwest Ames
OldTown - Old Town
SWISU - South & West of Iowa State University
Sawyer - Sawyer
SawyerW - Sawyer West
Somerst - Somerset
StoneBr - Stone Brook
Timber - Timberland
Veenker - Veenker
Condition1: Proximity to various conditions
Artery - Adjacent to arterial street
Feedr - Adjacent to feeder street
Norm - Normal
RRNn - Within 200' of North-South Railroad
RRAn - Adjacent to North-South Railroad
PosN - Near positive off-site feature--park, greenbelt, etc.
PosA - Adjacent to postive off-site feature
RRNe - Within 200' of East-West Railroad
RRAe - Adjacent to East-West Railroad
Condition2: Proximity to various conditions (if more than one is present)
Artery - Adjacent to arterial street
Feedr - Adjacent to feeder street
Norm - Normal
RRNn - Within 200' of North-South Railroad
RRAn - Adjacent to North-South Railroad
PosN - Near positive off-site feature--park, greenbelt, etc.
PosA - Adjacent to postive off-site feature
RRNe - Within 200' of East-West Railroad
RRAe - Adjacent to East-West Railroad
BldgType: Type of dwelling
1Fam - Single-family Detached
2FmCon - Two-family Conversion; originally built as one-family dwelling
Duplx - Duplex
TwnhsE - Townhouse End Unit
TwnhsI - Townhouse Inside Unit
HouseStyle: Style of dwelling
1Story - One story
1.5Fin - One and one-half story: 2nd level finished
1.5Unf - One and one-half story: 2nd level unfinished
2Story - Two story
2.5Fin - Two and one-half story: 2nd level finished
2.5Unf - Two and one-half story: 2nd level unfinished
SFoyer - Split Foyer
SLvl - Split Level
RoofStyle: Type of roof
Flat - Flat
Gable - Gable
Gambrel - Gabrel (Barn)
Hip - Hip
Mansard - Mansard
Shed - Shed
RoofMatl: Roof material
ClyTile - Clay or Tile
CompShg - Standard (Composite) Shingle
Membran - Membrane
Metal - Metal
Roll - Roll
Tar&Grv - Gravel & Tar
WdShake - Wood Shakes
WdShngl - Wood Shingles
Exterior1st: Exterior covering on house
AsbShng - Asbestos Shingles
AsphShn - Asphalt Shingles
BrkComm - Brick Common
BrkFace - Brick Face
CBlock - Cinder Block
CemntBd - Cement Board
HdBoard - Hard Board
ImStucc - Imitation Stucco
MetalSd - Metal Siding
Other - Other
Plywood - Plywood
PreCast - PreCast
Stone - Stone
Stucco - Stucco
VinylSd - Vinyl Siding
Wd - Wood Siding
WdShing - Wood Shingles
Exterior2nd: Exterior covering on house (if more than one material)
AsbShng - Asbestos Shingles
AsphShn - Asphalt Shingles
BrkComm - Brick Common
BrkFace - Brick Face
CBlock - Cinder Block
CemntBd - Cement Board
HdBoard - Hard Board
ImStucc - Imitation Stucco
MetalSd - Metal Siding
Other - Other
Plywood - Plywood
PreCast - PreCast
Stone - Stone
Stucco - Stucco
VinylSd - Vinyl Siding
Wd - Wood Siding
WdShing - Wood Shingles
MasVnrType: Masonry veneer type
BrkCmn - Brick Common
BrkFace - Brick Face
CBlock - Cinder Block
None - None
Stone - Stone
Foundation: Type of foundation
BrkTil - Brick & Tile
CBlock - Cinder Block
PConc - Poured Contrete
Slab - Slab
Stone - Stone
Wood - Wood
Heating: Type of heating
Floor - Floor Furnace
GasA - Gas forced warm air furnace
GasW - Gas hot water or steam heat
Grav - Gravity furnace
OthW - Hot water or steam heat other than gas
Wall - Wall furnace
CentralAir: Central air conditioning
N - No
Y - Yes
Electrical: Electrical system
SBrkr - Standard Circuit Breakers & Romex
FuseA - Fuse Box over 60 AMP and all Romex wiring (Average)
FuseF - 60 AMP Fuse Box and mostly Romex wiring (Fair)
FuseP - 60 AMP Fuse Box and mostly knob & tube wiring (poor)
Mix - Mixed
GarageType: Garage location
2Types - More than one type of garage
Attchd - Attached to home
Basment - Basement Garage
BuiltIn - Built-In (Garage part of house - typically has room above garage)
CarPort - Car Port
Detchd - Detached from home
NA - No Garage
SaleType: Type of sale
WD - Warranty Deed - Conventional
CWD - Warranty Deed - Cash
VWD - Warranty Deed - VA Loan
New - Home just constructed and sold
COD - Court Officer Deed/Estate
Con - Contract 15% Down payment regular terms
ConLw - Contract Low Down payment and low interest
ConLI - Contract Low Interest
ConLD - Contract Low Down
Oth - Other
SaleCondition: Condition of sale
Normal - Normal Sale
Abnorml - Abnormal Sale - trade, foreclosure, short sale
AdjLand - Adjoining Land Purchase
Alloca - Allocation - two linked properties with separate deeds, typically condo with a garage unit
Family - Sale between family members
Partial - Home was not completed when last assessed (associated with New Homes)
Distributions of categorical variables
# plot distributions of categorical variables
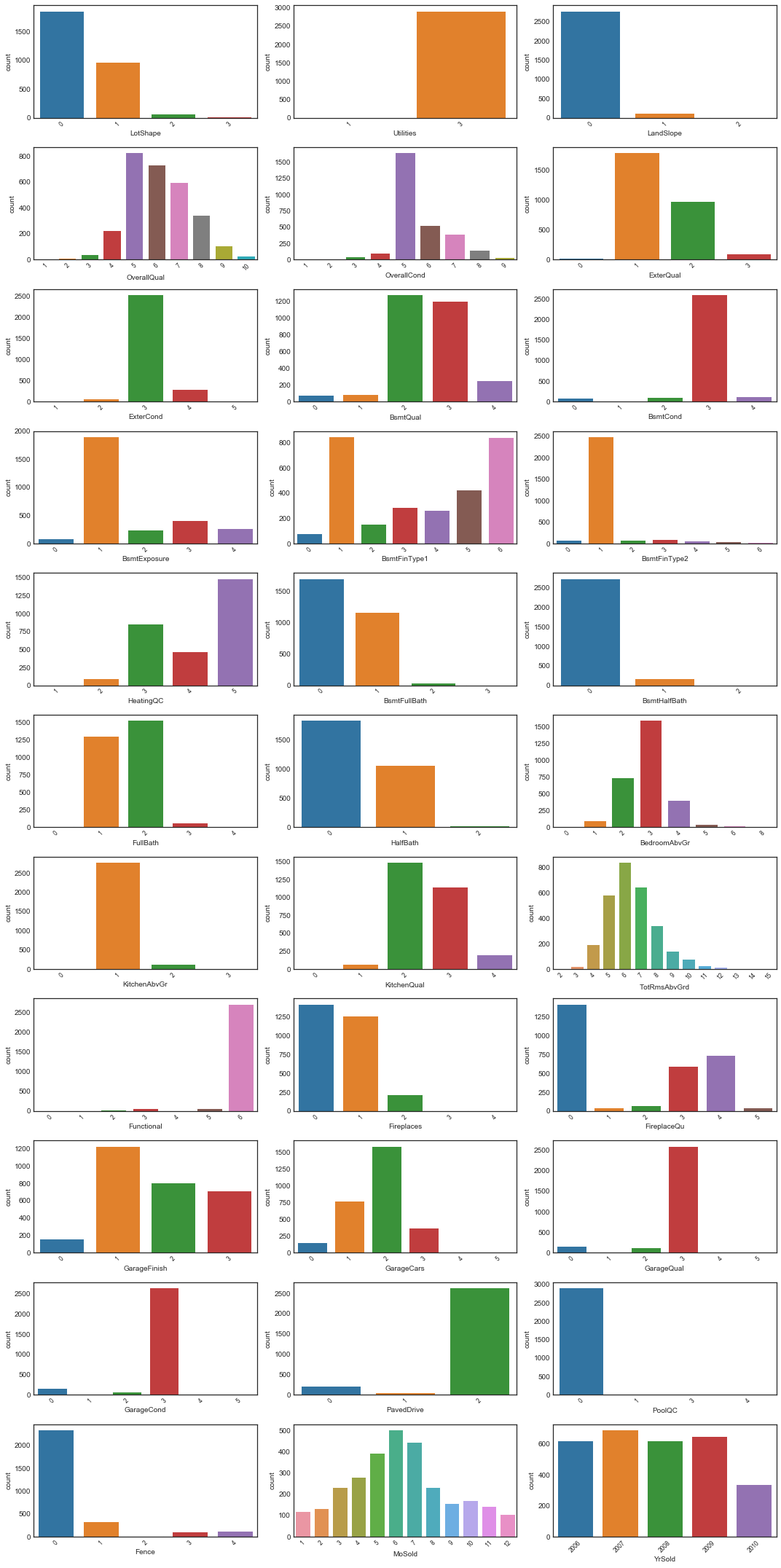
plot_discrete_dists(nrows=8, ncols=3, data=cats.data, figsize=(15, 30))
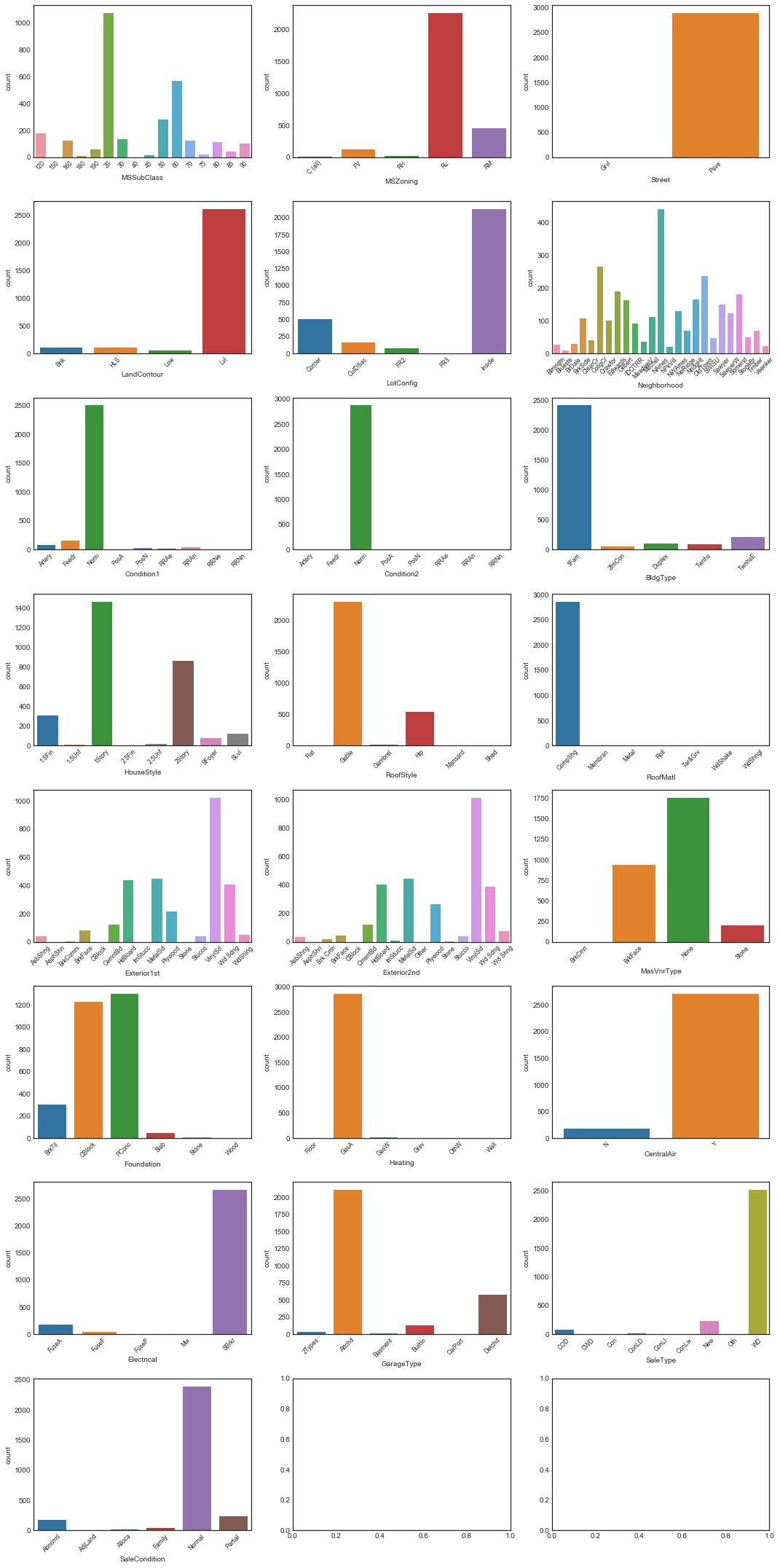
Some of these variables have highly unbalanced distributions. We’ll look for the most extremely unbalanced
# print distributions of categorical variables with more 90% concentration at single value
unbal_cat_cols = print_unbal_dists(data=cats.data, bal_threshold=0.9)
Pave 0.995885
Grvl 0.004115
Name: Street, dtype: float64
Norm 0.990055
Feedr 0.004458
Artery 0.001715
PosA 0.001372
PosN 0.001029
RRNn 0.000686
RRAn 0.000343
RRAe 0.000343
Name: Condition2, dtype: float64
CompShg 0.985940
Tar&Grv 0.007545
WdShake 0.003086
WdShngl 0.002401
Roll 0.000343
Metal 0.000343
Membran 0.000343
Name: RoofMatl, dtype: float64
GasA 0.984568
GasW 0.009259
Grav 0.003086
Wall 0.002058
OthW 0.000686
Floor 0.000343
Name: Heating, dtype: float64
Y 0.932785
N 0.067215
Name: CentralAir, dtype: float64
SBrkr 0.915295
FuseA 0.064472
FuseF 0.017147
FuseP 0.002743
Mix 0.000343
Name: Electrical, dtype: float64
Relationships among categorical variables
One often speaks loosely of “correlation” among variables to refer to statistical dependence. There are various measures of dependence, but here we rely on an information theoretic measure known as the variation of information. We discuss this measure briefly
The function
where is the joint entropy and the mutual information, defines a metric on a set of discrete random variables. Note that
which is sometimes called the “variation of information”. One can normalize to get a standardized variation of information
i.e. . Since is a metric, iff Furthermore, if and only if if and only if are independendent. So we can take as a “dependence distance”. The closer a variable is to , the more it depends on .
Of course, we don’t know the true distributions of the random variables in this data set, but the sample size is large enough that the sample distributions should be a good approximation.
We’ll look at the dependence distance among variables with feature selection in mind, namely the possibility of removing redundant variables.
# Get dataframe of dependence distances of categorical variables
cats_data_num = num_enc(data=cats.data)
cats_D_dep_df = D_dep(data=cats_data_num)
# plot all dependence distances
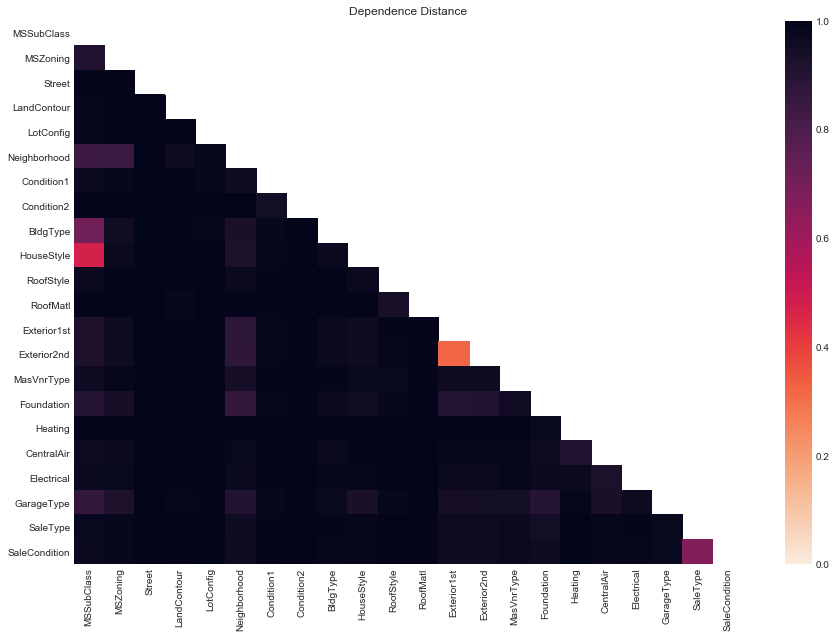
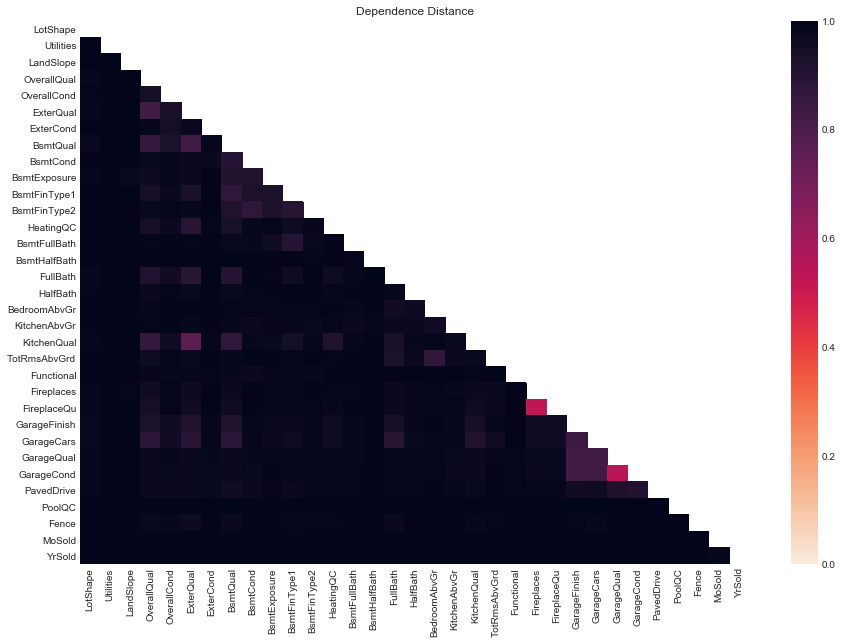
plot_D_dep(cats_D_dep_df, figsize=(15, 10))
# plot dependence distances less than 0.8
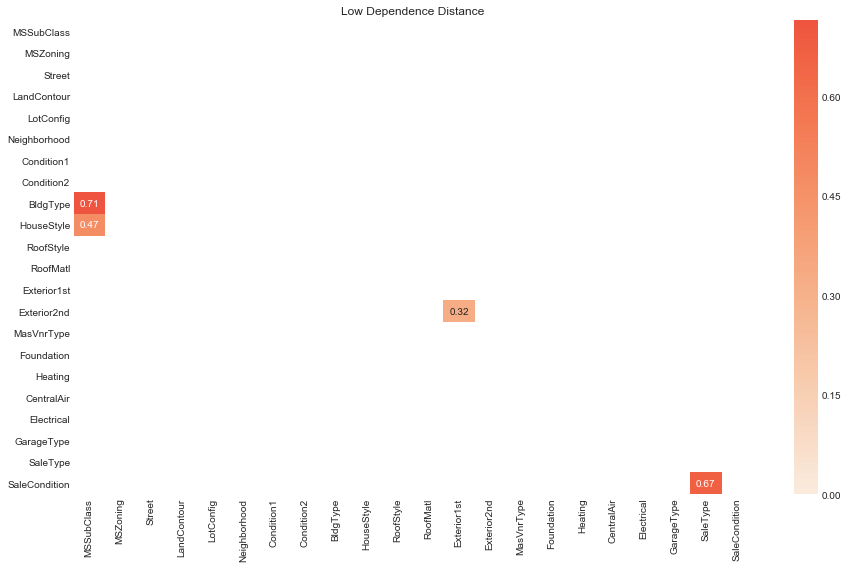
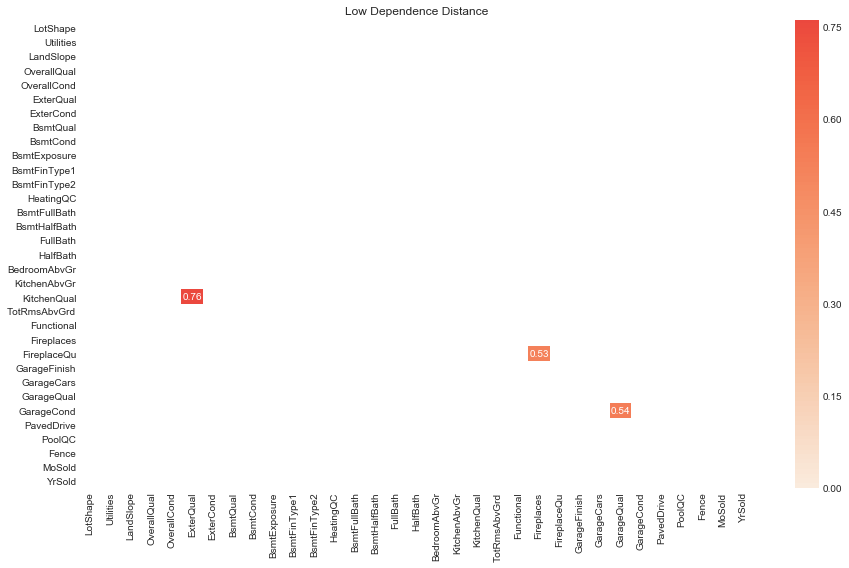
plot_low_D_dep(D_dep_df=cats_D_dep_df, D_threshold=0.8, figsize=(13, 8))
# rank categorical variables by dependence distance
rank_pairs_by_D(D_dep_df=cats_D_dep_df, D_threshold=0.8)
| var1 | var2 | D | |
|---|---|---|---|
| 1 | Exterior1st | Exterior2nd | 0.322737 |
| 2 | MSSubClass | HouseStyle | 0.472661 |
| 3 | SaleType | SaleCondition | 0.667950 |
| 4 | MSSubClass | BldgType | 0.714236 |
Notable pairs of distinct variables with low dependence distance are
Exterior1standExterior2ndhave the lowest dependence distance (). Their distributions are very similar and they have the same values. It probably makes more sense to think of them as close to identically distributed.MSSubclassandHouseStylehave the next lowest (). Inspecting their descriptions above we see that they have very similar categories, so they are measuring very similar things.BldgTypeandMSSubclass() are similar.MSSubclassandNeighborhood() are perhaps the first interesting pair in that they are measuring different things. We can imagine that the association between these two variables is somewhat strong – it makes sense that the size/age/type of house would be related to the neighborhood. Similarly,Exterior1st,Exterior2nd,MSZoning,Foundationalso have strong associations withNeighborhood.SaleConditionandSaleType() are also unsurprisingly associated.
Relationships between categoricals and SalePrice
Given that SalePrice seemed to be well-approximated by a log-normal distribution, we’ll measure dependence with log_SalePrice.
cats_data_num['log_SalePrice'] = np.log(clean.data['SalePrice'])
cats_data_num['log_SalePrice']
Id
train 1 12.247694
2 12.109011
3 12.317167
4 11.849398
5 12.429216
...
test 2915 NaN
2916 NaN
2917 NaN
2918 NaN
2919 NaN
Name: log_SalePrice, Length: 2916, dtype: float64
To visualize the relationship between the categorical variables and the response, we’ll look at the distributions of log_SalePrice over the values of the variables.
# violin plots of categorical variables vs. response
plot_violin_plots(nrows=8, ncols=3, data=cats_data_num, response='log_SalePrice', figsize=(15, 30))
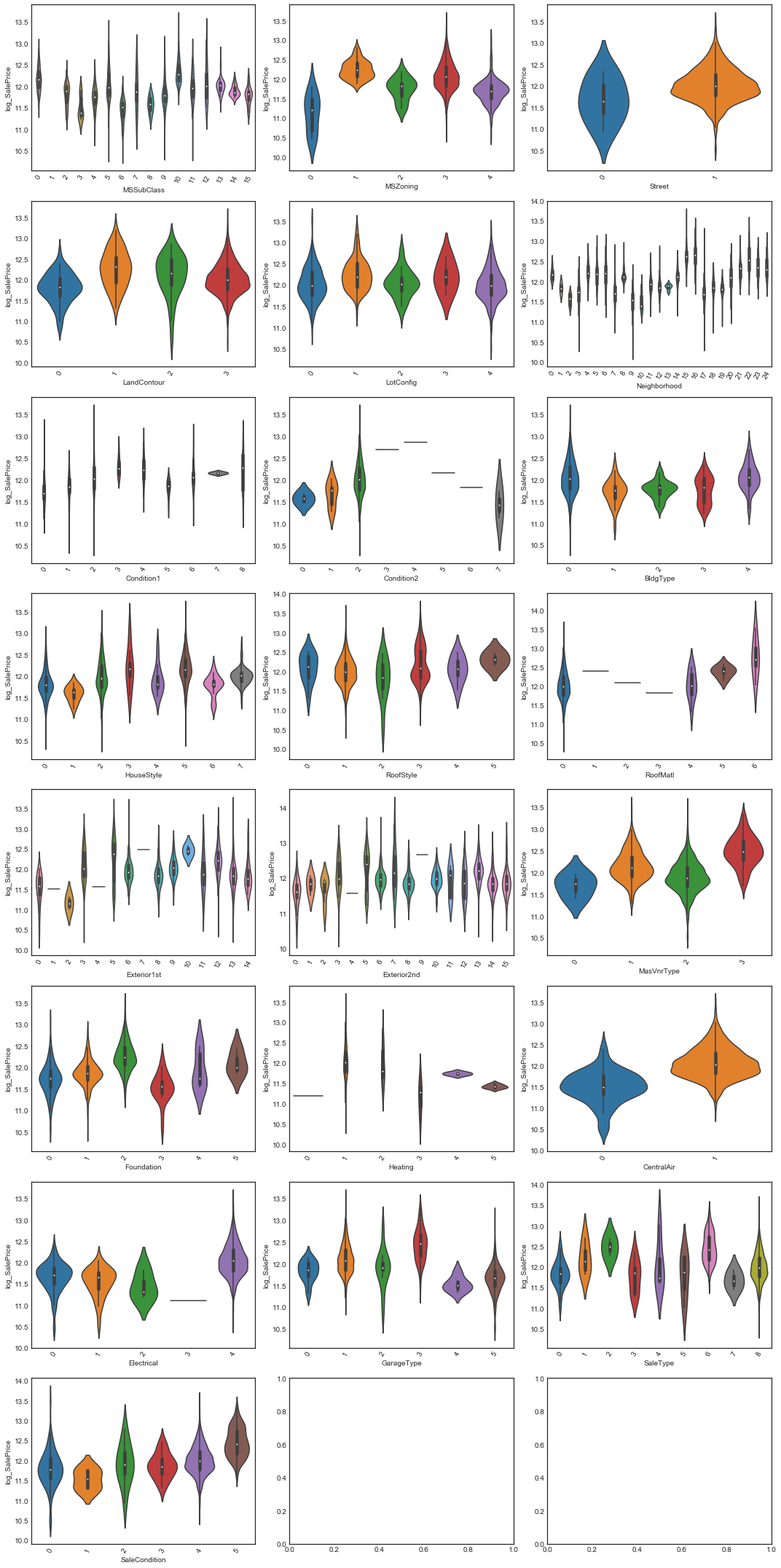
Note that horizontal lines for variable values in the violin plots indicate less than 5 observations having that value
From these plots, it’s difficult to determine with accuracy for which variables the distribution of log_SalePrice doesn’t seem to vary greatly across values (and hence are of low dependence and thus low predictive value). The dependence distance between the variables and log_SalePrice will provide additional information.
# rank categorical variables by dependence distance from response
D_dep_response(cats_data_num, 'log_SalePrice').sort_values(by='D').T
| Neighborhood | MSSubClass | Exterior2nd | Exterior1st | HouseStyle | Foundation | GarageType | MasVnrType | SaleCondition | LotConfig | ... | Condition1 | BldgType | RoofStyle | LandContour | Electrical | CentralAir | Heating | RoofMatl | Condition2 | Street | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0.713181 | 0.813289 | 0.831957 | 0.838796 | 0.894477 | 0.901514 | 0.919312 | 0.924422 | 0.926004 | 0.929782 | ... | 0.937908 | 0.938181 | 0.947682 | 0.956498 | 0.966163 | 0.973683 | 0.990074 | 0.990213 | 0.991566 | 0.996507 |
1 rows × 22 columns
The lower the dependence distance here, the better assocation with the response, hence the better the potential predictive value.
In particular, given how unbalanced their distributions are, it’s perhaps not too surprising to see RoofStyle, LandContour, Electrical and CentralAir all have such high dependence distance,
Ordinal variables
Now we’ll investigate ordinal variables, that is discrete variables with an ordering. In our cleaned dataframe these are variables with int64 dtype
# dataframe of ordinal variables
ords = HPDataFramePlus(data=clean.data.select_dtypes('int64'))
ords.data.head()
| LotShape | Utilities | LandSlope | OverallQual | OverallCond | ExterQual | ExterCond | BsmtQual | BsmtCond | BsmtExposure | ... | FireplaceQu | GarageFinish | GarageCars | GarageQual | GarageCond | PavedDrive | PoolQC | Fence | MoSold | YrSold | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | ||||||||||||||||||||||
| train | 1 | 0 | 3 | 0 | 7 | 5 | 2 | 3 | 3 | 3 | 1 | ... | 0 | 2 | 2 | 3 | 3 | 2 | 0 | 0 | 2 | 2008 |
| 2 | 0 | 3 | 0 | 6 | 8 | 1 | 3 | 3 | 3 | 4 | ... | 3 | 2 | 2 | 3 | 3 | 2 | 0 | 0 | 5 | 2007 | |
| 3 | 1 | 3 | 0 | 7 | 5 | 2 | 3 | 3 | 3 | 2 | ... | 3 | 2 | 2 | 3 | 3 | 2 | 0 | 0 | 9 | 2008 | |
| 4 | 1 | 3 | 0 | 7 | 5 | 1 | 3 | 2 | 4 | 1 | ... | 4 | 1 | 3 | 3 | 3 | 2 | 0 | 0 | 2 | 2006 | |
| 5 | 1 | 3 | 0 | 8 | 5 | 2 | 3 | 3 | 3 | 3 | ... | 3 | 2 | 3 | 3 | 3 | 2 | 0 | 0 | 12 | 2008 |
5 rows × 33 columns
ords.data.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 2916 entries, (train, 1) to (test, 2919)
Data columns (total 33 columns):
LotShape 2916 non-null int64
Utilities 2916 non-null int64
LandSlope 2916 non-null int64
OverallQual 2916 non-null int64
OverallCond 2916 non-null int64
ExterQual 2916 non-null int64
ExterCond 2916 non-null int64
BsmtQual 2916 non-null int64
BsmtCond 2916 non-null int64
BsmtExposure 2916 non-null int64
BsmtFinType1 2916 non-null int64
BsmtFinType2 2916 non-null int64
HeatingQC 2916 non-null int64
BsmtFullBath 2916 non-null int64
BsmtHalfBath 2916 non-null int64
FullBath 2916 non-null int64
HalfBath 2916 non-null int64
BedroomAbvGr 2916 non-null int64
KitchenAbvGr 2916 non-null int64
KitchenQual 2916 non-null int64
TotRmsAbvGrd 2916 non-null int64
Functional 2916 non-null int64
Fireplaces 2916 non-null int64
FireplaceQu 2916 non-null int64
GarageFinish 2916 non-null int64
GarageCars 2916 non-null int64
GarageQual 2916 non-null int64
GarageCond 2916 non-null int64
PavedDrive 2916 non-null int64
PoolQC 2916 non-null int64
Fence 2916 non-null int64
MoSold 2916 non-null int64
YrSold 2916 non-null int64
dtypes: int64(33)
memory usage: 783.3+ KB
We’ll print the description of all variables, however note that the print description contains the original value for the variables, while the cleaned dataframe clean contains the numerically encoded values
# print description of ordinal variables
ords.desc = desc
ords.print_desc(cols=ords.data.columns)
LotShape: General shape of property
Reg - Regular
IR1 - Slightly irregular
IR2 - Moderately Irregular
IR3 - Irregular
Utilities: Type of utilities available
AllPub - All public Utilities (E,G,W,& S)
NoSewr - Electricity, Gas, and Water (Septic Tank)
NoSeWa - Electricity and Gas Only
ELO - Electricity only
LandSlope: Slope of property
Gtl - Gentle slope
Mod - Moderate Slope
Sev - Severe Slope
OverallQual: Rates the overall material and finish of the house
10 - Very Excellent
9 - Excellent
8 - Very Good
7 - Good
6 - Above Average
5 - Average
4 - Below Average
3 - Fair
2 - Poor
1 - Very Poor
OverallCond: Rates the overall condition of the house
10 - Very Excellent
9 - Excellent
8 - Very Good
7 - Good
6 - Above Average
5 - Average
4 - Below Average
3 - Fair
2 - Poor
1 - Very Poor
ExterQual: Evaluates the quality of the material on the exterior
Ex - Excellent
Gd - Good
TA - Average/Typical
Fa - Fair
Po - Poor
ExterCond: Evaluates the present condition of the material on the exterior
Ex - Excellent
Gd - Good
TA - Average/Typical
Fa - Fair
Po - Poor
BsmtQual: Evaluates the height of the basement
Ex - Excellent (100+ inches)
Gd - Good (90-99 inches)
TA - Typical (80-89 inches)
Fa - Fair (70-79 inches)
Po - Poor (<70 inches
NA - No Basement
BsmtCond: Evaluates the general condition of the basement
Ex - Excellent
Gd - Good
TA - Typical - slight dampness allowed
Fa - Fair - dampness or some cracking or settling
Po - Poor - Severe cracking, settling, or wetness
NA - No Basement
BsmtExposure: Refers to walkout or garden level walls
Gd - Good Exposure
Av - Average Exposure (split levels or foyers typically score average or above)
Mn - Mimimum Exposure
No - No Exposure
NA - No Basement
BsmtFinType1: Rating of basement finished area
GLQ - Good Living Quarters
ALQ - Average Living Quarters
BLQ - Below Average Living Quarters
Rec - Average Rec Room
LwQ - Low Quality
Unf - Unfinshed
NA - No Basement
BsmtFinType2: Rating of basement finished area (if multiple types)
GLQ - Good Living Quarters
ALQ - Average Living Quarters
BLQ - Below Average Living Quarters
Rec - Average Rec Room
LwQ - Low Quality
Unf - Unfinshed
NA - No Basement
HeatingQC: Heating quality and condition
Ex - Excellent
Gd - Good
TA - Average/Typical
Fa - Fair
Po - Poor
BsmtFullBath: Basement full bathrooms
BsmtHalfBath: Basement half bathrooms
FullBath: Full bathrooms above grade
HalfBath: Half baths above grade
BedroomAbvGr: Bedrooms above grade (does NOT include basement bedrooms)
KitchenAbvGr: Kitchens above grade
KitchenQual: Kitchen quality
Ex - Excellent
Gd - Good
TA - Typical/Average
Fa - Fair
Po - Poor
TotRmsAbvGrd: Total rooms above grade (does not include bathrooms)
Functional: Home functionality (Assume typical unless deductions are warranted)
Typ - Typical Functionality
Min1 - Minor Deductions 1
Min2 - Minor Deductions 2
Mod - Moderate Deductions
Maj1 - Major Deductions 1
Maj2 - Major Deductions 2
Sev - Severely Damaged
Sal - Salvage only
Fireplaces: Number of fireplaces
FireplaceQu: Fireplace quality
Ex - Excellent - Exceptional Masonry Fireplace
Gd - Good - Masonry Fireplace in main level
TA - Average - Prefabricated Fireplace in main living area or Masonry Fireplace in basement
Fa - Fair - Prefabricated Fireplace in basement
Po - Poor - Ben Franklin Stove
NA - No Fireplace
GarageFinish: Interior finish of the garage
Fin - Finished
RFn - Rough Finished
Unf - Unfinished
NA - No Garage
GarageCars: Size of garage in car capacity
GarageQual: Garage quality
Ex - Excellent
Gd - Good
TA - Typical/Average
Fa - Fair
Po - Poor
NA - No Garage
GarageCond: Garage condition
Ex - Excellent
Gd - Good
TA - Typical/Average
Fa - Fair
Po - Poor
NA - No Garage
PavedDrive: Paved driveway
Y - Paved
P - Partial Pavement
N - Dirt/Gravel
PoolQC: Pool quality
Ex - Excellent
Gd - Good
TA - Average/Typical
Fa - Fair
NA - No Pool
Fence: Fence quality
GdPrv - Good Privacy
MnPrv - Minimum Privacy
GdWo - Good Wood
MnWw - Minimum Wood/Wire
NA - No Fence
MoSold: Month Sold (MM)
YrSold: Year Sold (YYYY)
Distributions of ordinal variables
# plot distributions of ordinal variables
plot_discrete_dists(nrows=11, ncols=3, data=ords.data, figsize=(15, 30))
# look at most unbalanced distributions
unbal_ord_cols = print_unbal_dists(data=ords.data, bal_threshold=0.9)
3 0.999657
1 0.000343
Name: Utilities, dtype: float64
0 0.951989
1 0.042524
2 0.005487
Name: LandSlope, dtype: float64
0 0.939986
1 0.058642
2 0.001372
Name: BsmtHalfBath, dtype: float64
1 0.954047
2 0.044239
0 0.001029
3 0.000686
Name: KitchenAbvGr, dtype: float64
6 0.931756
3 0.024005
5 0.021948
2 0.012003
4 0.006516
1 0.003086
0 0.000686
Name: Functional, dtype: float64
3 0.909122
0 0.054527
2 0.025377
4 0.005144
1 0.004801
5 0.001029
Name: GarageCond, dtype: float64
2 0.904664
0 0.074074
1 0.021262
Name: PavedDrive, dtype: float64
0 0.996914
4 0.001372
3 0.001029
1 0.000686
Name: PoolQC, dtype: float64
Relationships among ordinal variables
# get dataframe of dependence distances of ordinal variables
ords_D_dep_df = D_dep(ords.data)
# plot all dependence distances
plot_D_dep(D_dep_df=ords_D_dep_df, figsize=(15, 10))
# plot lower dependence distances of ordinal variables
plot_low_D_dep(D_dep_df=ords_D_dep_df, D_threshold=0.8, figsize=(13, 8))
# rank ordinals by low dependence distance
rank_pairs_by_D(D_dep_df=ords_D_dep_df, D_threshold=0.8)
| var1 | var2 | D | |
|---|---|---|---|
| 1 | Fireplaces | FireplaceQu | 0.528211 |
| 2 | GarageQual | GarageCond | 0.542600 |
| 3 | ExterQual | KitchenQual | 0.760176 |
Notable pairs of distinct ordinal variables with low dependence distance are
FireplacesandFireplaceQuhave the lowest dependence distance (). This is somewhat interesting, in that the quantities these variables are measuring are distinct (albeit related).GarageQualandGarageCondhave the next lowest (). Inspecting their descriptions above we see that they have very similar categories, so they are measuring very similar things. There is ostensibly a distinction between the quality of the garage and its condition, however.- Pairs of garage variables display relatively low dependence distance, as do pairs of basement variables and quality variables.
Relationships between ordinals and SalePrice
# add log_SalePrice to ordinal dataframe
ords.data['log_SalePrice'] = np.log(clean.data['SalePrice'])
ords.data['log_SalePrice']
Id
train 1 12.247694
2 12.109011
3 12.317167
4 11.849398
5 12.429216
...
test 2915 NaN
2916 NaN
2917 NaN
2918 NaN
2919 NaN
Name: log_SalePrice, Length: 2916, dtype: float64
# violin plots of ordinals
plot_violin_plots(11, 3, ords.data, 'log_SalePrice', figsize=(15, 30))

# plot dependence distance with log_SalePrice
D_dep_response(ords.data, 'log_SalePrice').sort_values(by='D').T
| MoSold | OverallQual | TotRmsAbvGrd | BsmtFinType1 | YrSold | GarageCars | BsmtQual | GarageFinish | FireplaceQu | OverallCond | ... | GarageQual | ExterCond | GarageCond | PavedDrive | Functional | BsmtHalfBath | LandSlope | KitchenAbvGr | PoolQC | Utilities | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0.795577 | 0.821511 | 0.83499 | 0.859118 | 0.877148 | 0.879704 | 0.879858 | 0.886311 | 0.886812 | 0.890191 | ... | 0.951855 | 0.957094 | 0.959353 | 0.962894 | 0.965643 | 0.978447 | 0.979514 | 0.981345 | 0.997317 | 0.999801 |
1 rows × 33 columns
Again variables with unbalanced distributions (e.g. PoolQc, Utilities) tend to have high dependence distance, as do variables for which the distribution of log_SalePrice doesn’t differ much across their classes (e.g. BsmtHalfBath, PavedDrive, LandSlope).
That OverallQual has high dependence with SalePrice isn’t surprising, but perhaps MoSold having the lowest is.
Rank correlation hypothesis tests
One way of testing statistical dependence between ordered varialbes is using rank correlations. Since they’re relatively straightforward to calculate, we calculate three common ones and compare. We’ll look at Pearson’s , Spearman’s , and Kendall’s
# rank correlation results as dataframes
rho_df = rank_hyp_test(ords, 'rho', ss.pearsonr)
r_s_df = rank_hyp_test(ords, 'r_s', ss.spearmanr)
tau_df = rank_hyp_test(ords, 'tau', ss.kendalltau)
rank_hyp_test_dfs = {'rho': rho_df, 'r_s': r_s_df, 'tau': tau_df}
# rank and sort by p-value of Pearson's rho
get_rank_corr_df(rank_hyp_test_dfs).drop(columns=['rho', 'r_s', 'tau']).sort_values(by='rho_p_val_rank')
| rho_p_val | rho_p_val_rank | r_s_p_val | r_s_p_val_rank | tau_p_val | tau_p_val_rank | |
|---|---|---|---|---|---|---|
| OverallQual | 0.000000e+00 | 1 | 0.000000e+00 | 1 | 5.929359e-270 | 1 |
| ExterQual | 7.761033e-201 | 2 | 2.040959e-203 | 3 | 1.272156e-159 | 4 |
| GarageCars | 3.307683e-199 | 3 | 2.382463e-207 | 2 | 6.327182e-176 | 2 |
| KitchenQual | 2.324509e-190 | 4 | 3.122308e-193 | 5 | 1.456887e-158 | 5 |
| BsmtQual | 5.427313e-175 | 5 | 2.488211e-197 | 4 | 1.250445e-164 | 3 |
| GarageFinish | 2.620057e-146 | 6 | 9.382754e-165 | 7 | 2.217914e-140 | 6 |
| FullBath | 1.759447e-141 | 7 | 3.253667e-167 | 6 | 1.117470e-133 | 7 |
| FireplaceQu | 3.528296e-114 | 8 | 7.777438e-110 | 8 | 1.384314e-99 | 9 |
| TotRmsAbvGrd | 3.524836e-110 | 9 | 4.199477e-108 | 9 | 5.527766e-104 | 8 |
| Fireplaces | 2.049485e-89 | 10 | 2.189811e-101 | 10 | 5.443444e-88 | 10 |
| HeatingQC | 2.503143e-82 | 11 | 2.833473e-89 | 11 | 5.700439e-81 | 11 |
| GarageQual | 1.143613e-46 | 12 | 1.501771e-43 | 13 | 2.160589e-41 | 13 |
| BsmtExposure | 3.598521e-45 | 13 | 1.337016e-41 | 15 | 1.843618e-40 | 14 |
| GarageCond | 5.806508e-45 | 14 | 1.512574e-40 | 16 | 2.197488e-38 | 16 |
| BsmtFinType1 | 1.544276e-39 | 15 | 2.791158e-46 | 12 | 2.122343e-46 | 12 |
| HalfBath | 6.573728e-35 | 16 | 9.576207e-42 | 14 | 3.530858e-39 | 15 |
| PavedDrive | 1.174245e-32 | 17 | 9.055822e-28 | 18 | 6.292790e-27 | 18 |
| LotShape | 3.682206e-29 | 18 | 3.397766e-36 | 17 | 1.363538e-34 | 17 |
| BsmtCond | 1.302478e-26 | 19 | 1.100259e-25 | 19 | 4.811484e-25 | 19 |
| BsmtFullBath | 5.765714e-20 | 20 | 4.174597e-18 | 21 | 1.040257e-17 | 21 |
| BedroomAbvGr | 5.553622e-16 | 21 | 6.069682e-20 | 20 | 2.027010e-20 | 20 |
| KitchenAbvGr | 1.568173e-08 | 22 | 2.543739e-10 | 23 | 3.235206e-10 | 23 |
| Functional | 1.437417e-07 | 23 | 9.116464e-08 | 24 | 9.253383e-08 | 24 |
| Fence | 2.386137e-05 | 24 | 4.477501e-13 | 22 | 1.551382e-12 | 22 |
| PoolQC | 1.030024e-03 | 25 | 1.490013e-02 | 27 | 1.492559e-02 | 27 |
| MoSold | 2.677357e-02 | 26 | 7.253421e-03 | 26 | 6.503260e-03 | 26 |
| ExterCond | 5.869885e-02 | 27 | 6.460164e-01 | 32 | 6.635896e-01 | 33 |
| YrSold | 1.550808e-01 | 28 | 2.543787e-01 | 30 | 2.573829e-01 | 30 |
| OverallCond | 1.567476e-01 | 29 | 6.717184e-07 | 25 | 1.787177e-07 | 25 |
| LandSlope | 1.671482e-01 | 30 | 7.277014e-02 | 28 | 7.323031e-02 | 28 |
| BsmtFinType2 | 5.861356e-01 | 31 | 1.246273e-01 | 29 | 1.412702e-01 | 29 |
| Utilities | 6.304159e-01 | 32 | 5.249597e-01 | 31 | 5.247749e-01 | 31 |
| BsmtHalfBath | 8.503143e-01 | 33 | 6.522158e-01 | 33 | 6.520497e-01 | 32 |
There is more or less good agreement of -value rankings among the rank correlation hypothesis tests. In particular for a 95% significance level all three fail to reject the null for MoSold, ExterCond, OverallCond, LandSlope, BsmtFinType2, Utilities and BsmtHalfBath. Applying a stricter value of 99.9% significance, all three reject PoolQC as well.
It’s important to recognize that rank correlation tests are measures of monotonicity (the tendency of variables to increase together and decrease together). They may fail to detect non-linear relationships that are not monotonic. In our particular case, MoSold had the highest statistical dependence with log_SalePrice among ordinal variables, but all three rank correlation tests reject a relationship between the two at 95% significance.
Quantitative variables
Finally we’ll consider the quantitative variables, that is the continuous variables. In our cleaned dataframe these are the variables with float64 dtype.
# dataframe of quantitative variables
quants = HPDataFramePlus(data=clean.data.select_dtypes('float64').drop(columns=['SalePrice']))
quants.data.head()
| LotFrontage | LotArea | YearBuilt | YearRemodAdd | MasVnrArea | BsmtFinSF1 | BsmtFinSF2 | BsmtUnfSF | TotalBsmtSF | 1stFlrSF | ... | GrLivArea | GarageYrBlt | GarageArea | WoodDeckSF | OpenPorchSF | EnclosedPorch | 3SsnPorch | ScreenPorch | PoolArea | MiscVal | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | ||||||||||||||||||||||
| train | 1 | 65.0 | 8450.0 | 2003.0 | 2003.0 | 196.0 | 706.0 | 0.0 | 150.0 | 856.0 | 856.0 | ... | 1710.0 | 2003.0 | 548.0 | 0.0 | 61.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 | 80.0 | 9600.0 | 1976.0 | 1976.0 | 0.0 | 978.0 | 0.0 | 284.0 | 1262.0 | 1262.0 | ... | 1262.0 | 1976.0 | 460.0 | 298.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 3 | 68.0 | 11250.0 | 2001.0 | 2002.0 | 162.0 | 486.0 | 0.0 | 434.0 | 920.0 | 920.0 | ... | 1786.0 | 2001.0 | 608.0 | 0.0 | 42.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 4 | 60.0 | 9550.0 | 1915.0 | 1970.0 | 0.0 | 216.0 | 0.0 | 540.0 | 756.0 | 961.0 | ... | 1717.0 | 1998.0 | 642.0 | 0.0 | 35.0 | 272.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 5 | 84.0 | 14260.0 | 2000.0 | 2000.0 | 350.0 | 655.0 | 0.0 | 490.0 | 1145.0 | 1145.0 | ... | 2198.0 | 2000.0 | 836.0 | 192.0 | 84.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
5 rows × 22 columns
quants.data.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 2916 entries, (train, 1) to (test, 2919)
Data columns (total 22 columns):
LotFrontage 2916 non-null float64
LotArea 2916 non-null float64
YearBuilt 2916 non-null float64
YearRemodAdd 2916 non-null float64
MasVnrArea 2916 non-null float64
BsmtFinSF1 2916 non-null float64
BsmtFinSF2 2916 non-null float64
BsmtUnfSF 2916 non-null float64
TotalBsmtSF 2916 non-null float64
1stFlrSF 2916 non-null float64
2ndFlrSF 2916 non-null float64
LowQualFinSF 2916 non-null float64
GrLivArea 2916 non-null float64
GarageYrBlt 2916 non-null float64
GarageArea 2916 non-null float64
WoodDeckSF 2916 non-null float64
OpenPorchSF 2916 non-null float64
EnclosedPorch 2916 non-null float64
3SsnPorch 2916 non-null float64
ScreenPorch 2916 non-null float64
PoolArea 2916 non-null float64
MiscVal 2916 non-null float64
dtypes: float64(22)
memory usage: 532.7+ KB
# print description of quantitative variables
quants.desc = desc
quants.print_desc(cols=quants.data.columns)
LotFrontage: Linear feet of street connected to property
LotArea: Lot size in square feet
YearBuilt: Original construction date
YearRemodAdd: Remodel date (same as construction date if no remodeling or additions)
MasVnrArea: Masonry veneer area in square feet
BsmtFinSF1: Type 1 finished square feet
BsmtFinSF2: Type 2 finished square feet
BsmtUnfSF: Unfinished square feet of basement area
TotalBsmtSF: Total square feet of basement area
1stFlrSF: First Floor square feet
2ndFlrSF: Second floor square feet
LowQualFinSF: Low quality finished square feet (all floors)
GrLivArea: Above grade (ground) living area square feet
GarageYrBlt: Year garage was built
GarageArea: Size of garage in square feet
WoodDeckSF: Wood deck area in square feet
OpenPorchSF: Open porch area in square feet
EnclosedPorch: Enclosed porch area in square feet
3SsnPorch: Three season porch area in square feet
ScreenPorch: Screen porch area in square feet
PoolArea: Pool area in square feet
MiscVal: $Value of miscellaneous feature
quants.data.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 2916 entries, (train, 1) to (test, 2919)
Data columns (total 22 columns):
LotFrontage 2916 non-null float64
LotArea 2916 non-null float64
YearBuilt 2916 non-null float64
YearRemodAdd 2916 non-null float64
MasVnrArea 2916 non-null float64
BsmtFinSF1 2916 non-null float64
BsmtFinSF2 2916 non-null float64
BsmtUnfSF 2916 non-null float64
TotalBsmtSF 2916 non-null float64
1stFlrSF 2916 non-null float64
2ndFlrSF 2916 non-null float64
LowQualFinSF 2916 non-null float64
GrLivArea 2916 non-null float64
GarageYrBlt 2916 non-null float64
GarageArea 2916 non-null float64
WoodDeckSF 2916 non-null float64
OpenPorchSF 2916 non-null float64
EnclosedPorch 2916 non-null float64
3SsnPorch 2916 non-null float64
ScreenPorch 2916 non-null float64
PoolArea 2916 non-null float64
MiscVal 2916 non-null float64
dtypes: float64(22)
memory usage: 532.7+ KB
# plot distributions of quantitative variables
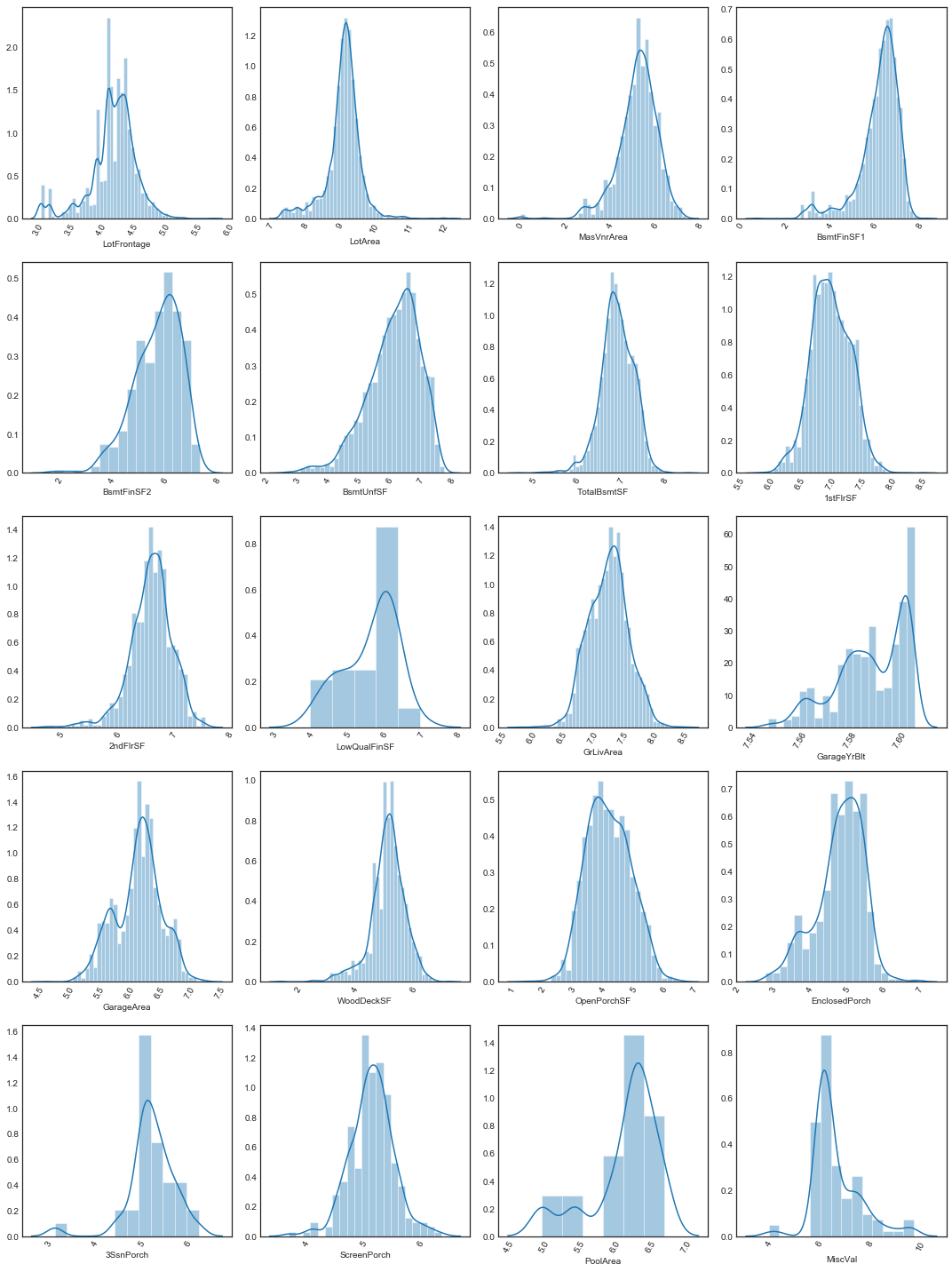
plot_cont_dists(nrows=6, ncols=4, data=quants.data, figsize=(15, 20))
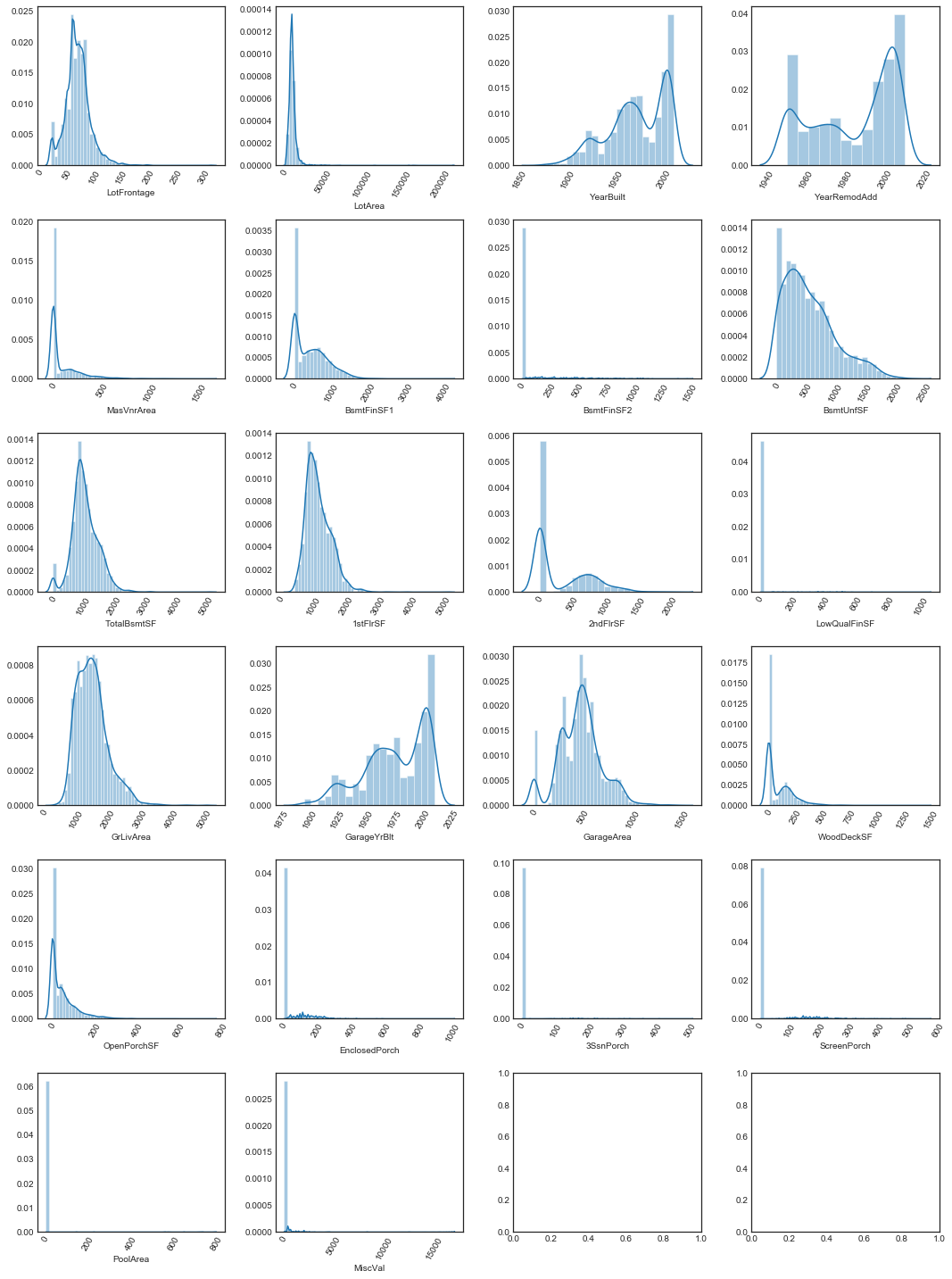
Most of the variables are highly positively skewed
quants.data.skew()
LotFrontage 1.049465
LotArea 13.269377
YearBuilt -0.600024
YearRemodAdd -0.449893
MasVnrArea 2.618990
BsmtFinSF1 0.982465
BsmtFinSF2 4.145816
BsmtUnfSF 0.919998
TotalBsmtSF 0.677494
1stFlrSF 1.259407
2ndFlrSF 0.861482
LowQualFinSF 12.088646
GrLivArea 1.069506
GarageYrBlt -0.658118
GarageArea 0.219101
WoodDeckSF 1.847119
OpenPorchSF 2.533111
EnclosedPorch 4.003630
3SsnPorch 11.375940
ScreenPorch 3.946335
PoolArea 17.694707
MiscVal 21.947201
dtype: float64
Some of the quantitative variables appear to be multimodal. For quite a few, this is due to a large peak at zero, and for some it’s clear that zero is being used as a stand-in for a null value (for example, PoolArea = 0 if the house has no pool). We’ll look at which variables have a high peak at zero
We note that many of these variables have long right tails, so logarithmic scales may be more appropriate for these.
# plot distributions of logarithms of all nonzero values of quantitative variables
log_cols = quants.data.columns.drop(['YearBuilt', 'YearRemodAdd'])
plot_log_cont_dists(nrows=5, ncols=4, data=quants.data, log_cols=log_cols, figsize=(15, 20))
Relationships among quantitative variables
# scatterplots of quantitative variables
sns.pairplot(quants.data)
<seaborn.axisgrid.PairGrid at 0x121036da0>
While pairplots can be helpful, this one is a bit too big to be of much use, although it may inform later methods of detecting relationships.
Some things do stand out:
-
There appear to be regions of exclusion for certain pairs of variables, probably due to impossible values. For example,
YrRemodAddis never greater thanYrBuilt. -
Many of the distributions are very concentrated.
LotArea,BsmtFinSF2,LowQualFinSF,EnclosedPorch,3SsnPorchall stand out as extremely concentrated.
Now we’ll look at dependencies among the quantitative variables
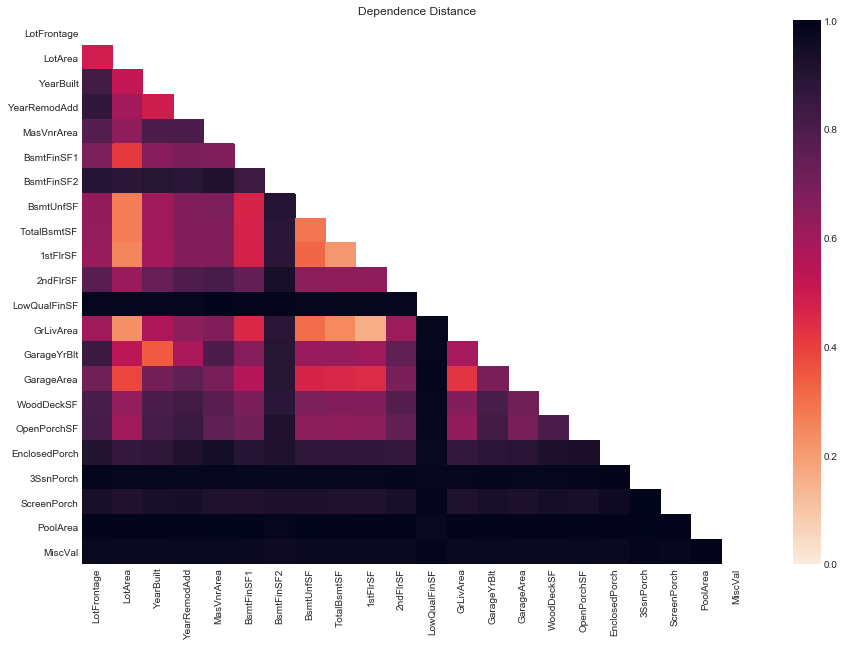
# dataframe of dependence distances of quantitative variables
quants_D_dep_df = D_dep(quants.data)
# plot dependence distance
plot_D_dep(D_dep_df=quants_D_dep_df, figsize=(15, 10))
# plot lower dependence distances of quantitative variables
plot_low_D_dep(D_dep_df=quants_D_dep_df, D_threshold=0.8, figsize=(13, 8))
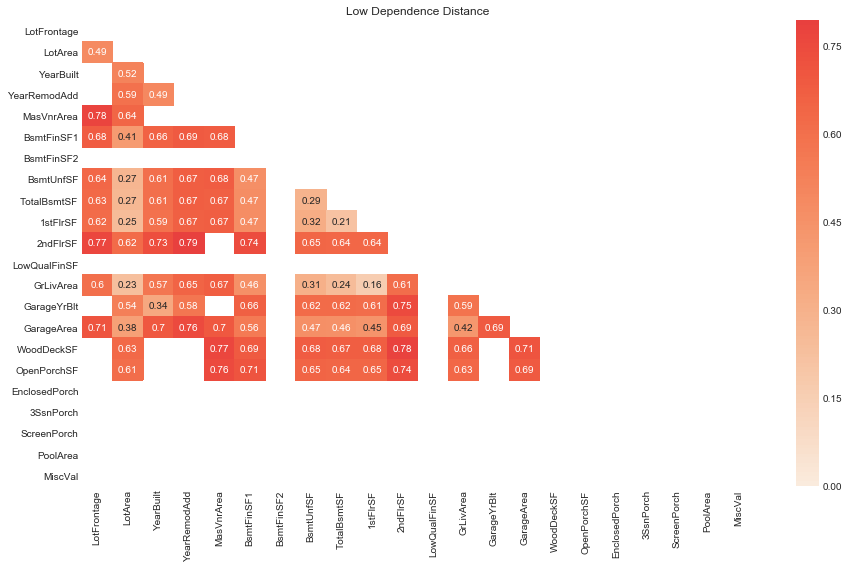
# display pairs of quantitatives with low dependence distance
rank_pairs_by_D(D_dep_df=quants_D_dep_df, D_threshold=0.8).head(10)
| var1 | var2 | D | |
|---|---|---|---|
| 1 | 1stFlrSF | GrLivArea | 0.158882 |
| 2 | TotalBsmtSF | 1stFlrSF | 0.213738 |
| 3 | LotArea | GrLivArea | 0.227010 |
| 4 | TotalBsmtSF | GrLivArea | 0.242833 |
| 5 | LotArea | 1stFlrSF | 0.250292 |
| 6 | LotArea | TotalBsmtSF | 0.269834 |
| 7 | LotArea | BsmtUnfSF | 0.273087 |
| 8 | BsmtUnfSF | TotalBsmtSF | 0.292260 |
| 9 | BsmtUnfSF | GrLivArea | 0.307987 |
| 10 | BsmtUnfSF | 1stFlrSF | 0.320845 |
Compared to quantitative and ordinal variables pairs, pairs of quantitative variables are showing much higher dependencies (lower dependence distances) overall. For many of these pairs , the high dependence makes sense given both variables are measuring very similar areas, for example, 1stFlrSF, GrLivArea and TotalBsmtSF.
We expect that Pearsons’ (i.e. correlation/linear dependence) of these variables should be high as well.
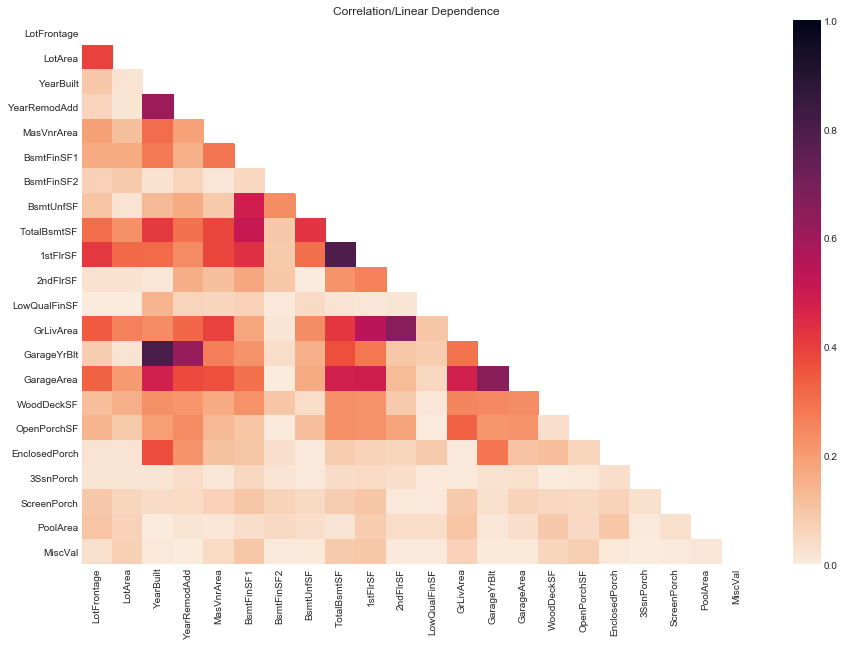
# plot pearson's correlation for quantitative variables
plot_corr(quants_data=quants.data, figsize=(15, 10))
# plot high absolute value of correlations of quantiatives
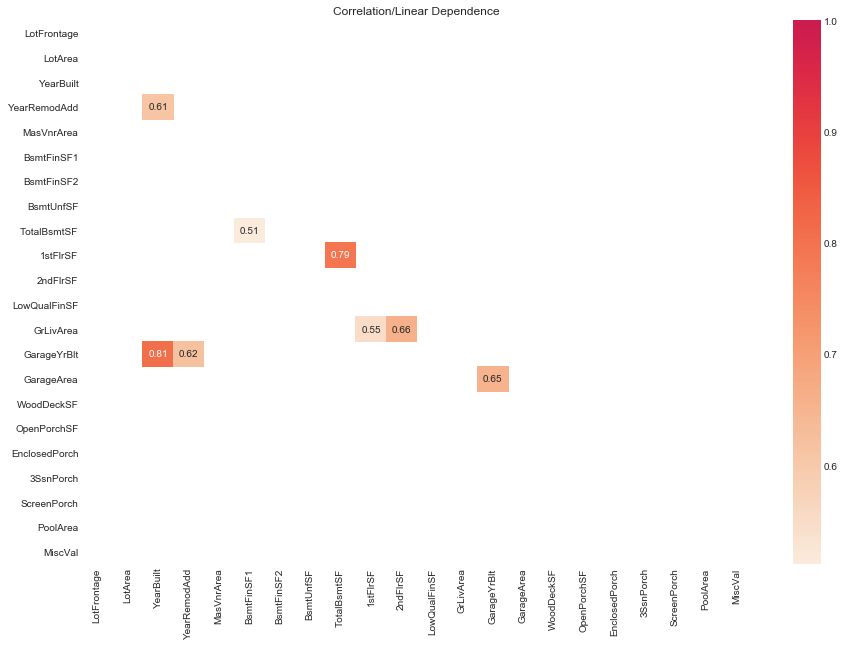
plot_high_corr(quants_data=quants.data, abs_corr_threshold=0.5, figsize=(15, 10))
# rank pairs of quantitatives by absolute values of correlation
rank_pairs_by_abs_corr_df = rank_pairs_by_abs_corr(quants_data=quants.data, abs_corr_threshold=0.5)
rank_pairs_by_abs_corr_df
| var1 | var2 | abs_corr | |
|---|---|---|---|
| 1 | BsmtFinSF1 | TotalBsmtSF | 0.511258 |
| 2 | 1stFlrSF | GrLivArea | 0.546383 |
| 3 | YearBuilt | YearRemodAdd | 0.612023 |
| 4 | YearRemodAdd | GarageYrBlt | 0.618881 |
| 5 | GarageYrBlt | GarageArea | 0.653440 |
| 6 | 2ndFlrSF | GrLivArea | 0.658420 |
| 7 | TotalBsmtSF | 1stFlrSF | 0.793482 |
| 8 | YearBuilt | GarageYrBlt | 0.808100 |
Relationships between quantitatives and SalePrice
# add log_SalePrice to quantitatives dataframe
quants.data['log_SalePrice'] = np.log(clean.data['SalePrice'])
quants.data['log_SalePrice']
Id
train 1 12.247694
2 12.109011
3 12.317167
4 11.849398
5 12.429216
...
test 2915 NaN
2916 NaN
2917 NaN
2918 NaN
2919 NaN
Name: log_SalePrice, Length: 2916, dtype: float64
# plot joint distributions of quantitative variables and log of sale price
plot_joint_dists_with_response(nrows=6, ncols=4, quants_data=quants.data, response='log_SalePrice', figsize=(15, 20))

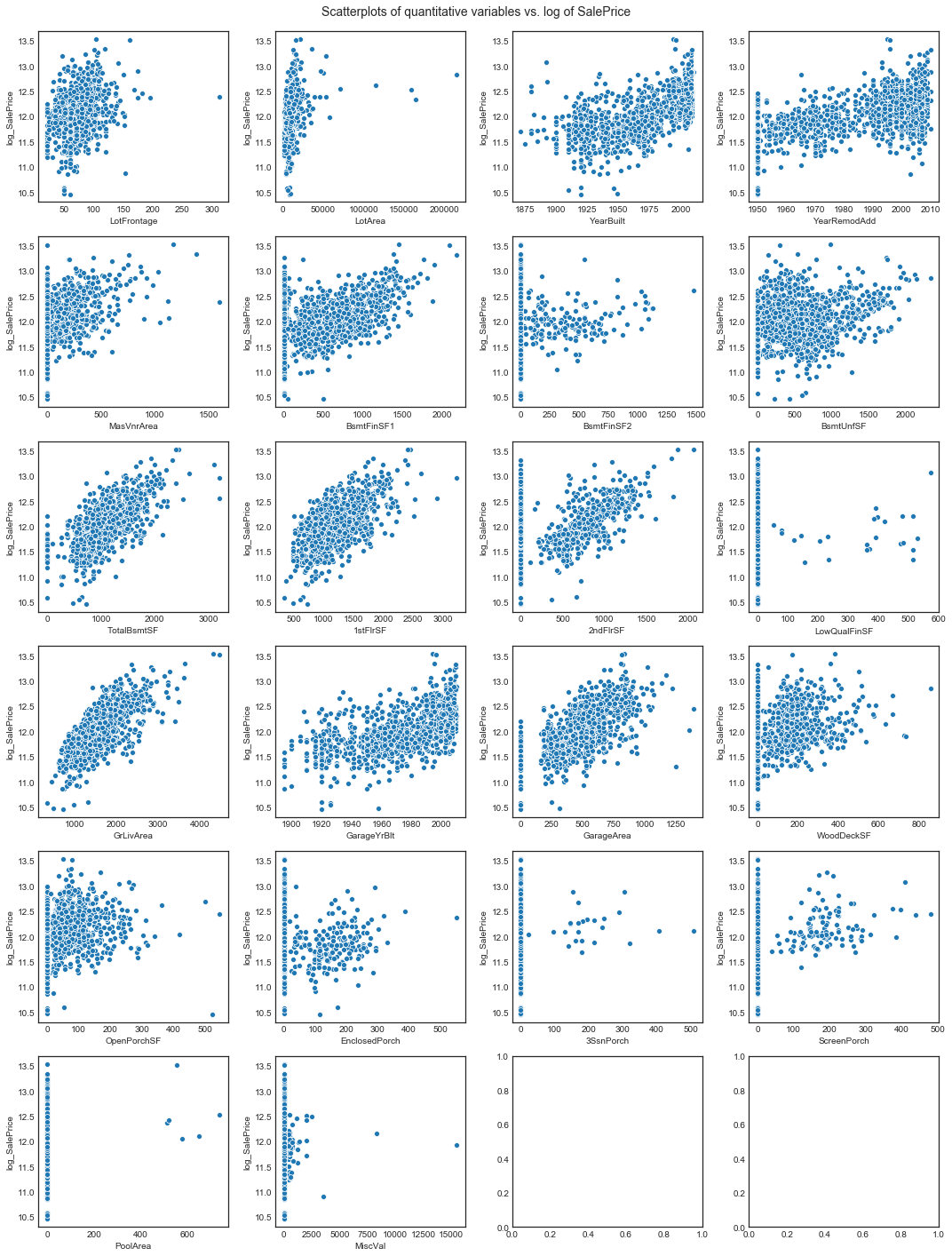
The distribution of some of the variables appears to be problematic for seaborn to fit a joint kernel density estimate. We’ll look at scatterplots instead
# scatterplots of quantitative variables and log of sale price
plot_scatter_with_response(nrows=6, ncols=4, quants_data=quants.data, response='log_SalePrice', figsize=(15, 20))
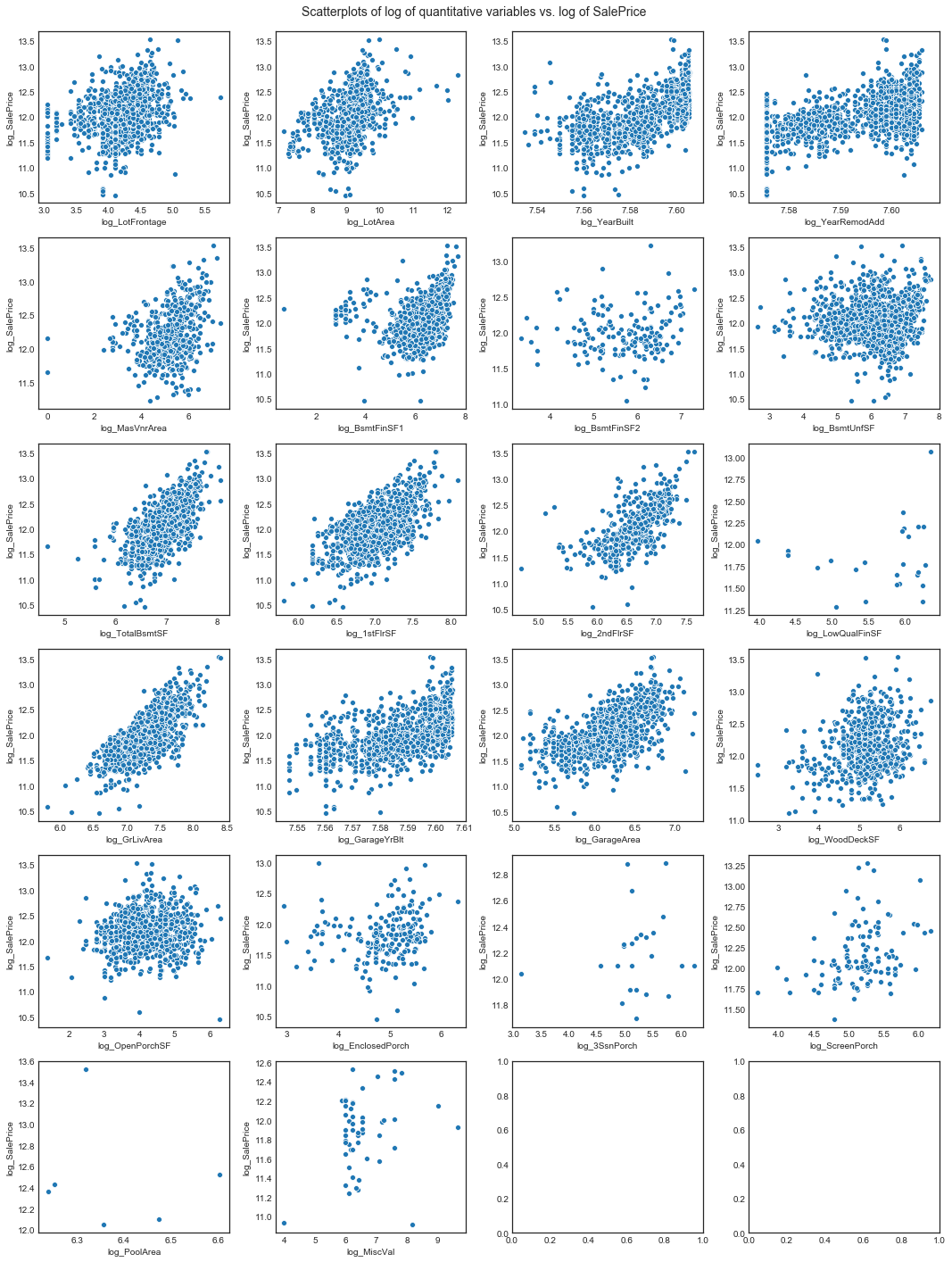
Now will look at scatterplots of log transformations of the quantitive variables vs. log_SalePrice
# scatterplots of log of nonzero values of quantitative variables and log of sale price
plot_log_scatter_with_response(nrows=6, ncols=4, quants_data=quants.data, response='log_SalePrice', figsize=(15, 20))
# rank dependence distance of quantiatives with log_SalePrice
D_dep_response(data=quants.data, response='log_SalePrice').sort_values(by='D').T
| LotArea | GrLivArea | 1stFlrSF | BsmtUnfSF | TotalBsmtSF | GarageArea | BsmtFinSF1 | YearBuilt | GarageYrBlt | LotFrontage | ... | YearRemodAdd | WoodDeckSF | MasVnrArea | EnclosedPorch | BsmtFinSF2 | ScreenPorch | MiscVal | LowQualFinSF | 3SsnPorch | PoolArea | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0.166598 | 0.216601 | 0.243486 | 0.259179 | 0.266558 | 0.390699 | 0.41101 | 0.549621 | 0.561122 | 0.579528 | ... | 0.627967 | 0.632256 | 0.647403 | 0.854684 | 0.875006 | 0.913641 | 0.968622 | 0.985514 | 0.98756 | 0.995242 |
1 rows × 22 columns
Considering the scatterplots and taking into account the dependence distance , we see that some quantitative variables appear likely to be less helpful in predicting SalePrice. Of these, EnclosedPorch, BsmtFinSF2, ScreenPorch, MiscVal, LowQualFinSF, 3SSnPorch, and PoolArea stand out (all have )