10. Unsupervised Learning
Exercise 10: PCA and K-means on simulated data
a. Generate data
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns; sns.set_style('whitegrid')
class_1 = np.random.uniform(low=0, high=1, size=1000).reshape(20, 50)
class_2 = np.random.uniform(low=0, high=2, size=1000).reshape(20, 50)
class_3 = np.random.uniform(low=0, high=3, size=1000).reshape(20, 50)
data = np.concatenate((class_1, class_2, class_3))
data = pd.DataFrame(data, columns=['X'+stri. for i in range(1, 51)])
data['class'] = 20*[1] + 20*[2] + 20*[3]
data.head()
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
... |
X42 |
X43 |
X44 |
X45 |
X46 |
X47 |
X48 |
X49 |
X50 |
class |
| 0 |
0.206085 |
0.548891 |
0.483345 |
0.430228 |
0.084926 |
0.457959 |
0.313941 |
0.796469 |
0.899392 |
0.140730 |
... |
0.803371 |
0.575263 |
0.868178 |
0.887051 |
0.659624 |
0.130191 |
0.271975 |
0.206966 |
0.272497 |
1 |
| 1 |
0.549837 |
0.654331 |
0.679153 |
0.088327 |
0.920253 |
0.721935 |
0.079815 |
0.816096 |
0.702062 |
0.390909 |
... |
0.082494 |
0.681500 |
0.621130 |
0.090764 |
0.630456 |
0.398784 |
0.879749 |
0.637703 |
0.653399 |
1 |
| 2 |
0.834361 |
0.807387 |
0.186267 |
0.497567 |
0.470530 |
0.965813 |
0.960205 |
0.917021 |
0.269370 |
0.246568 |
... |
0.649654 |
0.079688 |
0.064122 |
0.702819 |
0.312329 |
0.822282 |
0.177533 |
0.227268 |
0.157189 |
1 |
| 3 |
0.485799 |
0.830802 |
0.311301 |
0.787556 |
0.177693 |
0.451556 |
0.901479 |
0.970518 |
0.929537 |
0.944158 |
... |
0.504830 |
0.045807 |
0.168133 |
0.188069 |
0.998266 |
0.684840 |
0.206639 |
0.748141 |
0.650031 |
1 |
| 4 |
0.323639 |
0.559594 |
0.433228 |
0.981336 |
0.235406 |
0.479690 |
0.232493 |
0.950931 |
0.596846 |
0.113195 |
... |
0.502297 |
0.820850 |
0.542294 |
0.151900 |
0.723607 |
0.603645 |
0.119756 |
0.913848 |
0.466831 |
1 |
5 rows × 51 columns
b. PCA
from sklearn.decomposition import PCA
pca = PCA()
data_trans = pd.DataFrame(pca.fit_transform(data.drop(columns=['class'])),
columns=['Z'+stri. for i in range(1, 51)])
data_trans['class'] = 20*[1] + 20*[2] + 20*[3]
data_trans.head()
|
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Z7 |
Z8 |
Z9 |
Z10 |
... |
Z42 |
Z43 |
Z44 |
Z45 |
Z46 |
Z47 |
Z48 |
Z49 |
Z50 |
class |
| 0 |
-3.197494 |
0.205622 |
-0.441883 |
-0.256300 |
0.203960 |
-0.353133 |
0.472105 |
0.034966 |
0.026696 |
0.186835 |
... |
0.113655 |
0.031458 |
0.110456 |
-0.094083 |
-0.093648 |
0.194276 |
0.256539 |
0.055143 |
-0.003031 |
1 |
| 1 |
-3.377112 |
-0.388694 |
0.082136 |
0.362302 |
0.228215 |
0.261574 |
-0.501082 |
-0.484285 |
-0.150148 |
-0.440468 |
... |
0.057817 |
-0.178044 |
0.209686 |
0.150724 |
-0.132578 |
0.062330 |
-0.014915 |
-0.030767 |
0.006091 |
1 |
| 2 |
-3.962193 |
0.178716 |
0.212917 |
0.404123 |
-0.071486 |
0.267885 |
0.302552 |
-0.940849 |
-0.250239 |
-0.387476 |
... |
-0.383477 |
0.267378 |
-0.250597 |
-0.173644 |
0.058662 |
-0.110632 |
0.174202 |
-0.053465 |
0.030769 |
1 |
| 3 |
-2.973925 |
0.110673 |
-0.380835 |
0.118737 |
-0.252083 |
-0.154925 |
0.080041 |
-0.069936 |
-0.091114 |
0.446387 |
... |
0.076662 |
0.028786 |
0.345715 |
0.146093 |
0.171473 |
-0.248217 |
-0.094597 |
-0.127434 |
0.150054 |
1 |
| 4 |
-3.645312 |
0.102917 |
-0.161366 |
0.346589 |
0.374630 |
0.161183 |
-0.680470 |
0.095888 |
0.020735 |
0.602909 |
... |
0.176197 |
0.056955 |
0.274409 |
0.044277 |
0.098239 |
0.230063 |
0.273771 |
-0.051816 |
-0.029336 |
1 |
5 rows × 51 columns
sns.scatterplot(x=data_trans['Z1'], y=data_trans['Z2'], data=data,
hue='class', palette=sns.color_palette(n_colors=3))
<matplotlib.axes._subplots.AxesSubplot at 0x1a1aa72ac8>
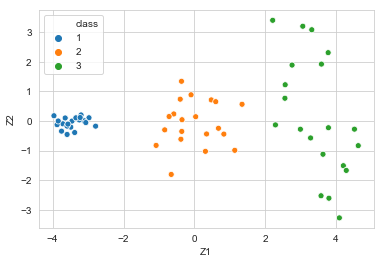
c. K-means clustering on full dataset with K=3
from sklearn.cluster import KMeans
kmeans3 = KMeans(n_clusters=3, random_state=0)
kmeans3.fit(data.drop(columns=['class']))
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=0, tol=0.0001, verbose=0)
class_labels = pd.DataFrame({'true': data['class'],
'K=3, full': kmeans3.labels_})
class_labels['K=3, full'].value_counts()
0 21
1 20
2 19
Name: K=3, full, dtype: int64
It appears that kmeans labeled clusters differently, so we’ll adjust. There’s a bit of guesswork but it appears the true cluster label → kmeans cluster label mapping is 1↦1,2↦0,3↦2.
map = {0:2, 1:1, 2:3}
class_labels.loc[:, 'K=3, full'] = [map[label] for label
in class_labels['K=3, full']]
# percentage of class labels kmeans got right
np.sum(class_labels['true'] == class_labels['K=3, full'])/60
d. K-means clustering on full dataset with K=2
kmeans2 = KMeans(n_clusters=2, random_state=0)
kmeans2.fit(data.drop(columns=['class']))
class_labels['K=2, full'] = kmeans2.labels_
class_labels['K=2, full'].value_counts()
1 31
0 29
Name: K=2, full, dtype: int64
class_labels[class_labels['true'] == 1]
|
true |
K=3, full |
K=2, full |
| 0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
1 |
1 |
1 |
| 3 |
1 |
1 |
1 |
| 4 |
1 |
1 |
1 |
| 5 |
1 |
1 |
1 |
| 6 |
1 |
1 |
1 |
| 7 |
1 |
1 |
1 |
| 8 |
1 |
1 |
1 |
| 9 |
1 |
1 |
1 |
| 10 |
1 |
1 |
1 |
| 11 |
1 |
1 |
1 |
| 12 |
1 |
1 |
1 |
| 13 |
1 |
1 |
1 |
| 14 |
1 |
1 |
1 |
| 15 |
1 |
1 |
1 |
| 16 |
1 |
1 |
1 |
| 17 |
1 |
1 |
1 |
| 18 |
1 |
1 |
1 |
| 19 |
1 |
1 |
1 |
class_labels[class_labels['true'] == 2]
|
true |
K=3, full |
K=2, full |
| 20 |
2 |
2 |
0 |
| 21 |
2 |
2 |
0 |
| 22 |
2 |
2 |
0 |
| 23 |
2 |
2 |
1 |
| 24 |
2 |
2 |
0 |
| 25 |
2 |
2 |
1 |
| 26 |
2 |
2 |
0 |
| 27 |
2 |
2 |
1 |
| 28 |
2 |
2 |
1 |
| 29 |
2 |
2 |
0 |
| 30 |
2 |
2 |
1 |
| 31 |
2 |
2 |
1 |
| 32 |
2 |
2 |
1 |
| 33 |
2 |
2 |
0 |
| 34 |
2 |
2 |
1 |
| 35 |
2 |
2 |
0 |
| 36 |
2 |
2 |
1 |
| 37 |
2 |
2 |
1 |
| 38 |
2 |
2 |
0 |
| 39 |
2 |
2 |
1 |
class_labels[class_labels['true'] == 2]['K=2, full'].value_counts()
1 11
0 9
Name: K=2, full, dtype: int64
class_labels[class_labels['true'] == 3]
|
true |
K=3, full |
K=2, full |
| 40 |
3 |
2 |
0 |
| 41 |
3 |
2 |
0 |
| 42 |
3 |
2 |
0 |
| 43 |
3 |
2 |
0 |
| 44 |
3 |
2 |
0 |
| 45 |
3 |
2 |
0 |
| 46 |
3 |
2 |
0 |
| 47 |
3 |
2 |
0 |
| 48 |
3 |
2 |
0 |
| 49 |
3 |
2 |
0 |
| 50 |
3 |
2 |
0 |
| 51 |
3 |
2 |
0 |
| 52 |
3 |
0 |
0 |
| 53 |
3 |
2 |
0 |
| 54 |
3 |
2 |
0 |
| 55 |
3 |
2 |
0 |
| 56 |
3 |
2 |
0 |
| 57 |
3 |
2 |
0 |
| 58 |
3 |
2 |
0 |
| 59 |
3 |
2 |
0 |
For K=2, the algorithm correctly separated classes 1 and 3, and assigned class 2 to class 1 and 3 in roughly equal proportion.
e. K-means clustering on full dataset with K=4
kmeans4 = KMeans(n_clusters=4, random_state=0)
kmeans4.fit(data.drop(columns=['class']))
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=4, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=0, tol=0.0001, verbose=0)
class_labels['K=4, full'] = kmeans4.labels_
class_labels['K=4, full'].value_counts()
0 20
2 19
3 18
1 3
Name: K=4, full, dtype: int64
class_labels[class_labels['K=4, full'] == 0]
|
true |
K=3, full |
K=2, full |
K=4, full |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
1 |
1 |
1 |
0 |
| 2 |
1 |
1 |
1 |
0 |
| 3 |
1 |
1 |
1 |
0 |
| 4 |
1 |
1 |
1 |
0 |
| 5 |
1 |
1 |
1 |
0 |
| 6 |
1 |
1 |
1 |
0 |
| 7 |
1 |
1 |
1 |
0 |
| 8 |
1 |
1 |
1 |
0 |
| 9 |
1 |
1 |
1 |
0 |
| 10 |
1 |
1 |
1 |
0 |
| 11 |
1 |
1 |
1 |
0 |
| 12 |
1 |
1 |
1 |
0 |
| 13 |
1 |
1 |
1 |
0 |
| 14 |
1 |
1 |
1 |
0 |
| 15 |
1 |
1 |
1 |
0 |
| 16 |
1 |
1 |
1 |
0 |
| 17 |
1 |
1 |
1 |
0 |
| 18 |
1 |
1 |
1 |
0 |
| 19 |
1 |
1 |
1 |
0 |
class_labels[class_labels['K=4, full'] == 1]
|
true |
K=3, full |
K=2, full |
K=4, full |
| 48 |
3 |
2 |
0 |
1 |
| 58 |
3 |
2 |
0 |
1 |
| 59 |
3 |
2 |
0 |
1 |
class_labels[class_labels['K=4, full'] == 2]
|
true |
K=3, full |
K=2, full |
K=4, full |
| 20 |
2 |
0 |
0 |
2 |
| 21 |
2 |
0 |
0 |
2 |
| 22 |
2 |
0 |
0 |
2 |
| 23 |
2 |
0 |
1 |
2 |
| 24 |
2 |
0 |
0 |
2 |
| 25 |
2 |
0 |
1 |
2 |
| 26 |
2 |
0 |
0 |
2 |
| 27 |
2 |
0 |
1 |
2 |
| 28 |
2 |
0 |
1 |
2 |
| 29 |
2 |
0 |
0 |
2 |
| 30 |
2 |
0 |
1 |
2 |
| 31 |
2 |
0 |
1 |
2 |
| 32 |
2 |
0 |
1 |
2 |
| 34 |
2 |
0 |
1 |
2 |
| 35 |
2 |
0 |
0 |
2 |
| 36 |
2 |
0 |
1 |
2 |
| 37 |
2 |
0 |
1 |
2 |
| 38 |
2 |
0 |
0 |
2 |
| 39 |
2 |
0 |
1 |
2 |
class_labels[class_labels['K=4, full'] == 3]
|
true |
K=3, full |
K=2, full |
K=4, full |
| 33 |
2 |
0 |
0 |
3 |
| 40 |
3 |
2 |
0 |
3 |
| 41 |
3 |
2 |
0 |
3 |
| 42 |
3 |
2 |
0 |
3 |
| 43 |
3 |
2 |
0 |
3 |
| 44 |
3 |
2 |
0 |
3 |
| 45 |
3 |
2 |
0 |
3 |
| 46 |
3 |
2 |
0 |
3 |
| 47 |
3 |
2 |
0 |
3 |
| 49 |
3 |
2 |
0 |
3 |
| 50 |
3 |
2 |
0 |
3 |
| 51 |
3 |
2 |
0 |
3 |
| 52 |
3 |
0 |
0 |
3 |
| 53 |
3 |
2 |
0 |
3 |
| 54 |
3 |
2 |
0 |
3 |
| 55 |
3 |
2 |
0 |
3 |
| 56 |
3 |
2 |
0 |
3 |
| 57 |
3 |
2 |
0 |
3 |
K=4 almost correctly identified clusters 1, 2, and 3. The exception was a fourth cluster formed from 3 observations from class 3 (presumably very close to each other).
f. K-means clustering on first two principal components with K=3
kmeans3_pca = KMeans(n_clusters=3, random_state=0)
kmeans3_pca.fit(data_trans[['Z1','Z2']])
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=0, tol=0.0001, verbose=0)
class_labels['K=3, pca'] = kmeans3_pca.labels_
class_labels['K=3, pca'].value_counts()
2 20
1 20
0 20
Name: K=3, pca, dtype: int64
class_labels[class_labels['true'] == 1]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
| 0 |
1 |
1 |
1 |
0 |
2 |
| 1 |
1 |
1 |
1 |
0 |
2 |
| 2 |
1 |
1 |
1 |
0 |
2 |
| 3 |
1 |
1 |
1 |
0 |
2 |
| 4 |
1 |
1 |
1 |
0 |
2 |
| 5 |
1 |
1 |
1 |
0 |
2 |
| 6 |
1 |
1 |
1 |
0 |
2 |
| 7 |
1 |
1 |
1 |
0 |
2 |
| 8 |
1 |
1 |
1 |
0 |
2 |
| 9 |
1 |
1 |
1 |
0 |
2 |
| 10 |
1 |
1 |
1 |
0 |
2 |
| 11 |
1 |
1 |
1 |
0 |
2 |
| 12 |
1 |
1 |
1 |
0 |
2 |
| 13 |
1 |
1 |
1 |
0 |
2 |
| 14 |
1 |
1 |
1 |
0 |
2 |
| 15 |
1 |
1 |
1 |
0 |
2 |
| 16 |
1 |
1 |
1 |
0 |
2 |
| 17 |
1 |
1 |
1 |
0 |
2 |
| 18 |
1 |
1 |
1 |
0 |
2 |
| 19 |
1 |
1 |
1 |
0 |
2 |
class_labels[class_labels['true'] == 2]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
| 20 |
2 |
0 |
0 |
2 |
0 |
| 21 |
2 |
0 |
0 |
2 |
0 |
| 22 |
2 |
0 |
0 |
2 |
0 |
| 23 |
2 |
0 |
1 |
2 |
0 |
| 24 |
2 |
0 |
0 |
2 |
0 |
| 25 |
2 |
0 |
1 |
2 |
0 |
| 26 |
2 |
0 |
0 |
2 |
0 |
| 27 |
2 |
0 |
1 |
2 |
0 |
| 28 |
2 |
0 |
1 |
2 |
0 |
| 29 |
2 |
0 |
0 |
2 |
0 |
| 30 |
2 |
0 |
1 |
2 |
0 |
| 31 |
2 |
0 |
1 |
2 |
0 |
| 32 |
2 |
0 |
1 |
2 |
0 |
| 33 |
2 |
0 |
0 |
3 |
0 |
| 34 |
2 |
0 |
1 |
2 |
0 |
| 35 |
2 |
0 |
0 |
2 |
0 |
| 36 |
2 |
0 |
1 |
2 |
0 |
| 37 |
2 |
0 |
1 |
2 |
0 |
| 38 |
2 |
0 |
0 |
2 |
0 |
| 39 |
2 |
0 |
1 |
2 |
0 |
class_labels[class_labels['true'] == 3]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
| 40 |
3 |
2 |
0 |
3 |
1 |
| 41 |
3 |
2 |
0 |
3 |
1 |
| 42 |
3 |
2 |
0 |
3 |
1 |
| 43 |
3 |
2 |
0 |
3 |
1 |
| 44 |
3 |
2 |
0 |
3 |
1 |
| 45 |
3 |
2 |
0 |
3 |
1 |
| 46 |
3 |
2 |
0 |
3 |
1 |
| 47 |
3 |
2 |
0 |
3 |
1 |
| 48 |
3 |
2 |
0 |
1 |
1 |
| 49 |
3 |
2 |
0 |
3 |
1 |
| 50 |
3 |
2 |
0 |
3 |
1 |
| 51 |
3 |
2 |
0 |
3 |
1 |
| 52 |
3 |
0 |
0 |
3 |
1 |
| 53 |
3 |
2 |
0 |
3 |
1 |
| 54 |
3 |
2 |
0 |
3 |
1 |
| 55 |
3 |
2 |
0 |
3 |
1 |
| 56 |
3 |
2 |
0 |
3 |
1 |
| 57 |
3 |
2 |
0 |
3 |
1 |
| 58 |
3 |
2 |
0 |
1 |
1 |
| 59 |
3 |
2 |
0 |
1 |
1 |
This time K=3 perfectly separated the classes
g. K-means clustering on scaled dataset with K=3
data_sc = data/data.std()
kmeans3_sc = KMeans(n_clusters=3, random_state=0)
kmeans3_sc.fit(data_sc.drop(columns=['class']))
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=0, tol=0.0001, verbose=0)
class_labels['K=3, scaled'] = kmeans3_sc.labels_
class_labels['K=3, scaled'].value_counts()
0 27
2 22
1 11
Name: K=3, scaled, dtype: int64
class_labels[class_labels['true'] == 1]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
K=3, scaled |
| 0 |
1 |
1 |
1 |
0 |
2 |
0 |
| 1 |
1 |
1 |
1 |
0 |
2 |
0 |
| 2 |
1 |
1 |
1 |
0 |
2 |
0 |
| 3 |
1 |
1 |
1 |
0 |
2 |
0 |
| 4 |
1 |
1 |
1 |
0 |
2 |
0 |
| 5 |
1 |
1 |
1 |
0 |
2 |
0 |
| 6 |
1 |
1 |
1 |
0 |
2 |
0 |
| 7 |
1 |
1 |
1 |
0 |
2 |
0 |
| 8 |
1 |
1 |
1 |
0 |
2 |
0 |
| 9 |
1 |
1 |
1 |
0 |
2 |
0 |
| 10 |
1 |
1 |
1 |
0 |
2 |
0 |
| 11 |
1 |
1 |
1 |
0 |
2 |
0 |
| 12 |
1 |
1 |
1 |
0 |
2 |
0 |
| 13 |
1 |
1 |
1 |
0 |
2 |
0 |
| 14 |
1 |
1 |
1 |
0 |
2 |
0 |
| 15 |
1 |
1 |
1 |
0 |
2 |
0 |
| 16 |
1 |
1 |
1 |
0 |
2 |
0 |
| 17 |
1 |
1 |
1 |
0 |
2 |
0 |
| 18 |
1 |
1 |
1 |
0 |
2 |
0 |
| 19 |
1 |
1 |
1 |
0 |
2 |
0 |
class_labels[class_labels['true'] == 2]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
K=3, scaled |
| 20 |
2 |
0 |
0 |
2 |
0 |
2 |
| 21 |
2 |
0 |
0 |
2 |
0 |
2 |
| 22 |
2 |
0 |
0 |
2 |
0 |
2 |
| 23 |
2 |
0 |
1 |
2 |
0 |
0 |
| 24 |
2 |
0 |
0 |
2 |
0 |
2 |
| 25 |
2 |
0 |
1 |
2 |
0 |
2 |
| 26 |
2 |
0 |
0 |
2 |
0 |
2 |
| 27 |
2 |
0 |
1 |
2 |
0 |
2 |
| 28 |
2 |
0 |
1 |
2 |
0 |
0 |
| 29 |
2 |
0 |
0 |
2 |
0 |
2 |
| 30 |
2 |
0 |
1 |
2 |
0 |
0 |
| 31 |
2 |
0 |
1 |
2 |
0 |
0 |
| 32 |
2 |
0 |
1 |
2 |
0 |
0 |
| 33 |
2 |
0 |
0 |
3 |
0 |
2 |
| 34 |
2 |
0 |
1 |
2 |
0 |
0 |
| 35 |
2 |
0 |
0 |
2 |
0 |
2 |
| 36 |
2 |
0 |
1 |
2 |
0 |
2 |
| 37 |
2 |
0 |
1 |
2 |
0 |
0 |
| 38 |
2 |
0 |
0 |
2 |
0 |
2 |
| 39 |
2 |
0 |
1 |
2 |
0 |
2 |
class_labels[class_labels['true'] == 3]
|
true |
K=3, full |
K=2, full |
K=4, full |
K=3, pca |
K=3, scaled |
| 40 |
3 |
2 |
0 |
3 |
1 |
2 |
| 41 |
3 |
2 |
0 |
3 |
1 |
2 |
| 42 |
3 |
2 |
0 |
3 |
1 |
2 |
| 43 |
3 |
2 |
0 |
3 |
1 |
1 |
| 44 |
3 |
2 |
0 |
3 |
1 |
1 |
| 45 |
3 |
2 |
0 |
3 |
1 |
2 |
| 46 |
3 |
2 |
0 |
3 |
1 |
1 |
| 47 |
3 |
2 |
0 |
3 |
1 |
2 |
| 48 |
3 |
2 |
0 |
1 |
1 |
1 |
| 49 |
3 |
2 |
0 |
3 |
1 |
2 |
| 50 |
3 |
2 |
0 |
3 |
1 |
1 |
| 51 |
3 |
2 |
0 |
3 |
1 |
1 |
| 52 |
3 |
0 |
0 |
3 |
1 |
2 |
| 53 |
3 |
2 |
0 |
3 |
1 |
1 |
| 54 |
3 |
2 |
0 |
3 |
1 |
2 |
| 55 |
3 |
2 |
0 |
3 |
1 |
1 |
| 56 |
3 |
2 |
0 |
3 |
1 |
1 |
| 57 |
3 |
2 |
0 |
3 |
1 |
2 |
| 58 |
3 |
2 |
0 |
1 |
1 |
1 |
| 59 |
3 |
2 |
0 |
1 |
1 |
1 |
These results are much worse than in part b.. However, this algorithm is highly sensitive to the random initialization - in practice setting a different random seed produces wildly different results. An averaging should be undertaken to reliably compare performance.
