islr notes and exercises from An Introduction to Statistical Learning

9. Support Vector Machines

Exercise 5: Nonlinear decision boundary with logistic regression and nonlinear feature transformation

%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_style('whitegrid')
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)

a. Generate data

X_1, X_2 = np.random.uniform(size=500) - 0.5, np.random.uniform(size=500) - 0.5
Y = np.sign(X_1**2 - X_2**2)

data = pd.DataFrame({'X_1': X_1, 'X_2': X_2, 'Y': Y})
data.head()
X_1 X_2 Y
0 0.314655 0.347183 -1.0
1 0.042885 -0.171818 -1.0
2 -0.365191 -0.486412 -1.0
3 -0.284827 -0.241447 1.0
4 -0.061084 -0.190989 -1.0

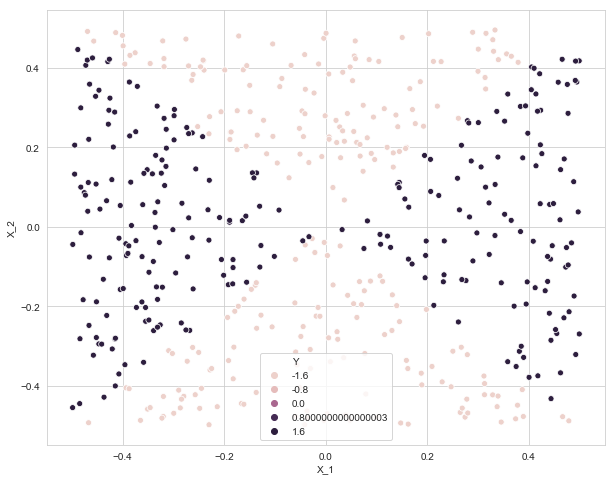
b. Scatterplot

plt.figure(figsize=(10, 8))
sns.scatterplot(x=data['X_1'], y=data['X_2'], data=data, hue='Y')

<matplotlib.axes._subplots.AxesSubplot at 0x1a1b95db70>

png

c. Train linear Logistic Regression model

Here we fit a logistic regression model P(Y=k)=exp⁡(β0+β1X1+β2X2) P(Y = k) = \exp(\beta_0 + \beta_1 X_1 + \beta_2 X_2)

from sklearn.linear_model import LogisticRegression

linear_logit = LogisticRegression()
linear_logit.fit(data[['X_1', 'X_2']], data['Y'])

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=None, solver='warn',
          tol=0.0001, verbose=0, warm_start=False)

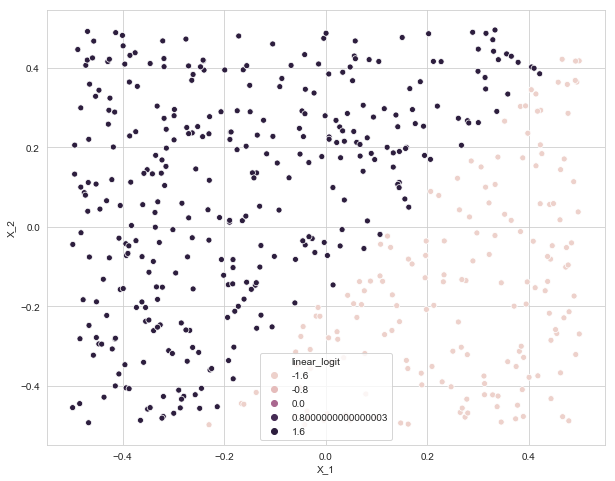
d. Linear logistic regression model prediction for training data

data['linear_logit'] = linear_logit.predict(data[['X_1', 'X_2']])


plt.figure(figsize=(10, 8))
sns.scatterplot(x=data['X_1'], y=data['X_2'], data=data, hue='linear_logit')

<matplotlib.axes._subplots.AxesSubplot at 0x1a1c960e48>

png

e. Train nonlinear logisitic regression models

We’ll train a model

P(Y=k)=exp⁡(β0+β1X1+β2X2+β3X12+β4X22+β5X1X2+β6log⁡(∣X1∣)+β7log⁡(∣X2∣)+β8log⁡(∣X1X2∣))P(Y = k) = \exp\left(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1^2 + \beta_4 X_2^2 + \beta_5 X_1X_2 + \beta_6 \log(|X_1|) + \beta_7 \log(|X_2|) + \beta_8 \log(|X_1 X_2|) \right)

# transform data
trans_data = data[['X_1', 'X_2']].copy()
trans_data['X_1^2'] = data['X_1']**2
trans_data['X_2^2'] = data['X_2']**2
trans_data['X_1X_2'] = data['X_1']*data['X_2']
trans_data['log(X_1)'] = np.log(np.absolute(trans_data[['X_1']]))
trans_data['log(X_2)'] = np.log(np.absolute(trans_data[['X_2']]))
trans_data['log(X_1X_2)'] = np.log(np.absolute(trans_data[['X_1X_2']]))
trans_data['Y'] = data['Y']
trans_data.head()
X_1 X_2 X_1^2 X_2^2 X_1X_2 log(X_1) log(X_2) log(X_1X_2) Y
0 0.314655 0.347183 0.099008 0.120536 0.109243 -1.156278 -1.057902 -2.214180 -1.0
1 0.042885 -0.171818 0.001839 0.029521 -0.007368 -3.149226 -1.761322 -4.910548 -1.0
2 -0.365191 -0.486412 0.133364 0.236596 0.177633 -1.007335 -0.720700 -1.728035 -1.0
3 -0.284827 -0.241447 0.081126 0.058297 0.068771 -1.255874 -1.421104 -2.676979 1.0
4 -0.061084 -0.190989 0.003731 0.036477 0.011666 -2.795504 -1.655540 -4.451044 -1.0 
# fit model
nonlinear_logit = LogisticRegression()
nonlinear_logit.fit(trans_data.drop(columns=['Y']), trans_data['Y'])

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=None, solver='warn',
          tol=0.0001, verbose=0, warm_start=False)

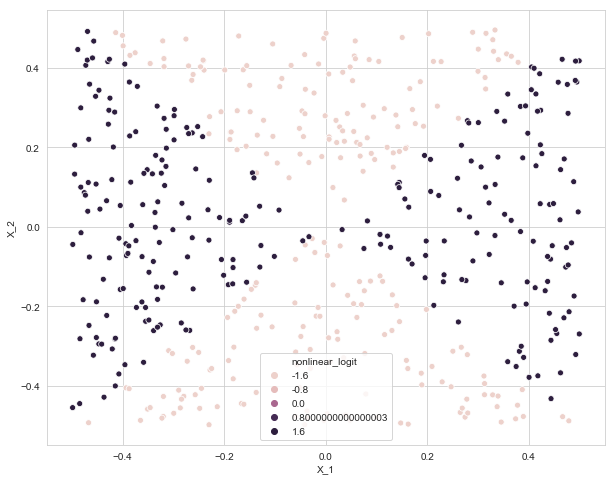
f. Nonlinear logistic regression model prediction for training data

trans_data['nonlinear_logit'] = nonlinear_logit.predict(trans_data.drop(columns=['Y']))

plt.figure(figsize=(10, 8))
sns.scatterplot(x=trans_data['X_1'], y=trans_data['X_2'], data=trans_data, hue='nonlinear_logit')

<matplotlib.axes._subplots.AxesSubplot at 0x1a1caaa780>

png

g. Train linear SVC and get prediction for training data

from sklearn.svm import SVC

linear_svc = SVC(kernel='linear')
linear_svc.fit(data.drop(columns=['Y']), data['Y'])

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
  kernel='linear', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)

data['linear_svc'] = linear_svc.predict(data.drop(columns=['Y']))

plt.figure(figsize=(10, 8))
sns.scatterplot(x=data['X_1'], y=data['X_2'], data=data, hue='linear_svc')

<matplotlib.axes._subplots.AxesSubplot at 0x1a1cc38eb8>

png

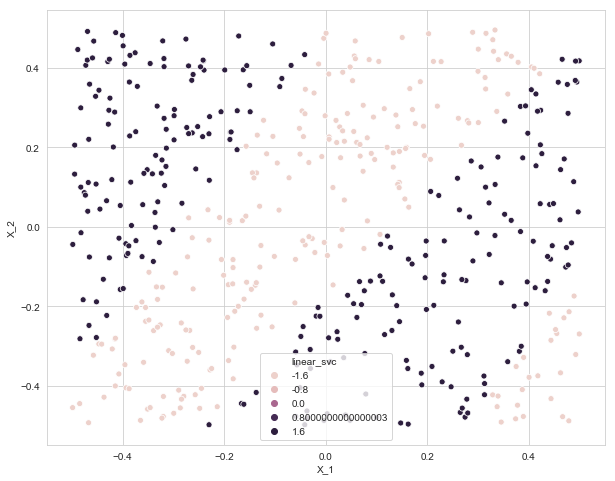
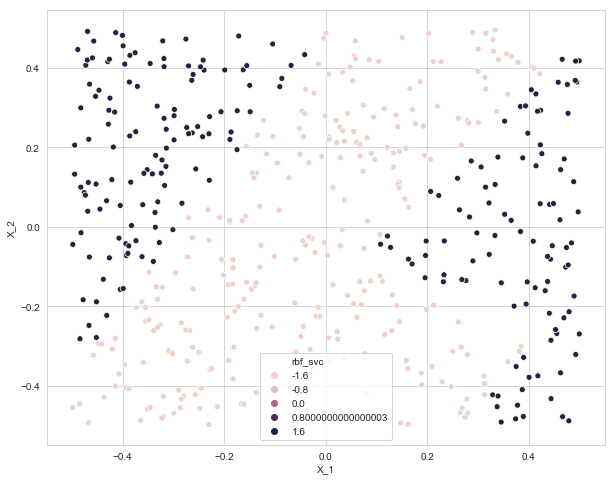
h. Train nonlinear SVM and get prediction for training data

rbf_svc = SVC(kernel='rbf')
rbf_svc.fit(data.drop(columns=['Y']), data['Y'])

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
  kernel='rbf', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)

data['rbf_svc'] = rbf_svc.predict(data.drop(columns=['Y']))

plt.figure(figsize=(10, 8))
sns.scatterplot(x=data['X_1'], y=data['X_2'], data=data, hue='rbf_svc')

<matplotlib.axes._subplots.AxesSubplot at 0x1a1cdd05f8>

png