islr notes and exercises from An Introduction to Statistical Learning

8. Tree-based Methods

Conceptual Exercises

Exercise 1: An example partition/decision tree.

Skip.

Exercise 2: Why a boosted stump leads to an additive model

The final form of the boosting model (see algorithm 8.12) is

f^(X)=∑b=1Bλf^b(x)\hat{f}(X) = \sum_{b = 1}^B \lambda \hat{f}^b(x)

Since the model is a stump (d=1d=1), for each bb the estimate is a function of a single predcitor, that is f^b(X)=f^b(Xj)\hat{f}^b(X) = \hat{f}^b(X_j) for some jb∈{1,…,p}j_b \in \{1, \dots, p\}. We can then collect terms:

f^(X)=∑b=1Bλf^b(Xjb)=∑j=1pλf^j(Xj) \begin{aligned} \hat{f}(X) &= \sum_{b = 1}^B \lambda \hat{f}^b(X_{j_b})\\ &= \sum_{j = 1}^p \lambda \hat{f}_j(X_j) \end{aligned}

where f^j(x)=∑λf^b(Xj)\hat{f}_j(x) = \sum \lambda \hat{f}^b(X_j) is a sum over all boosted trees which have XjX_j as a predictor.

This is the estimate of an additive model.

f(X)=∑j=1pfj(Xj)f(X) = \sum_{j=1}^p f_j(X_j)

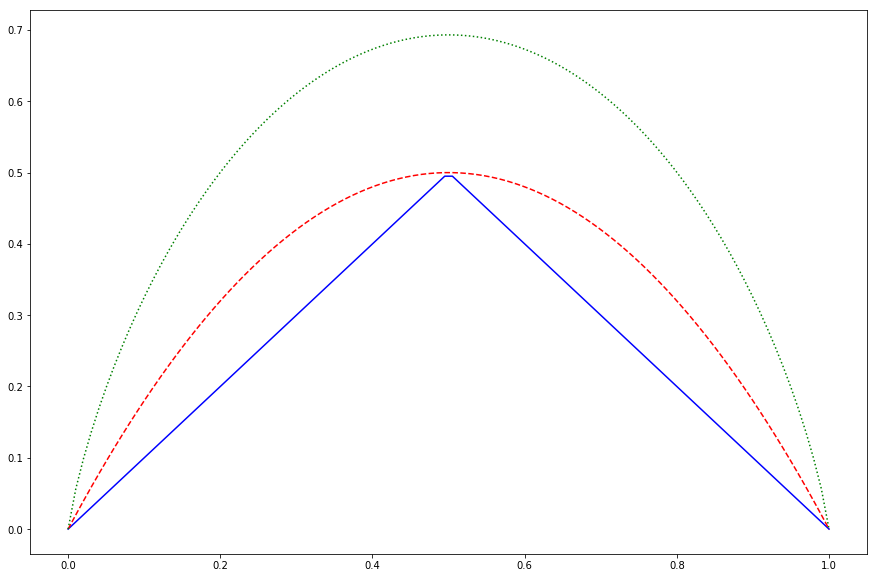
Exercise 3: Plotting classification error, Gini index, and entropy as functions of p^m1\hat{p}_{m1} for the two class case

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

def class_error(p_hat_m1):
    p_hat_m2 = 1 - p_hat_m1
    return 1 - p_hat_m2 if p_hat_m2 >= p_hat_m1 else 1 - p_hat_m1

def gini_index(p_hat_m1):
    p_hat_m2 = 1 - p_hat_m1
    return p_hat_m1 * ( 1 - p_hat_m1) + p_hat_m2 * ( 1 - p_hat_m2)

def entropy(p_hat_m1):
    p_hat_m2 = 1 - p_hat_m1
    if p_hat_m1 in {0, 1}:
        return 0
    else:
        return - np.sum(p_hat_m1 * np.log(p_hat_m1) + p_hat_m2 * np.log(p_hat_m2))

v_class_error = np.vectorize(class_error)
v_gini_index = np.vectorize(gini_index)
v_entropy = np.vectorize(entropy, otypes=[np.float])

x = np.linspace(0, 1, 100)
y_1, y_2, y_3  = v_class_error(x), v_gini_index(x), v_entropy(x)

fig, ax = plt.subplots(figsize=(15, 10))
ax.plot(x, y_1, '-b', label="Classification error")
ax.plot(x, y_2, '--r', label="Gini index")
ax.plot(x, y_3, ':g', label="Entropy")


[<matplotlib.lines.Line2D at 0x11ee4c550>]

png

Exercise 4: Sketching trees and partitions

Skip

Exercise 5: Combining bootstrap classification tree predictions

The 10 boostrap estimates for P(Red∣X)P(Red|X) are

p_est = np.array([0.1, 0.15, 0.2, 0.2, 0.55, 0.6, 0.6, 0.65, 0.7, 0.75])
p_est

array([0.1 , 0.15, 0.2 , 0.2 , 0.55, 0.6 , 0.6 , 0.65, 0.7 , 0.75])

First we find the classification based on majority vote

# boolean showing if predicted class is red
is_class_red = p_est >= 0.5
# number of times red is predicted
num_red_pred = np.sum(is_class_red)
# predict red if red is the majority vote
if num_red_pred/len(p_est) >= 0.5:
    maj_pred = "Red"
else:
    maj_pred = "Green"

f'majority prediction is {maj_pred}'

'majority prediction is Red'

Next we find the classification based on the average

if np.sum(p_est) >= 0.5:
    avg_pred = "Red"
else:
    avg_pred = "Green"

f'average prediction is {avg_pred}'

'average prediction is Red'

Exercise 6: A detailed explanation of recursive binary decision tree algorithm for linear regression

See our explanation in the notes for § 8.1.1