islr notes and exercises from An Introduction to Statistical Learning
7. Moving Beyond Linearity
Exercise 11: Exploring backfitting for multiple linear regression
a. Generating some data
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_style('whitegrid')
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
np.random.seed(27)
X_1, X_2, e = np.random.normal(loc=4, scale=2, size=100, ), np.random.exponential(size=100), np.random.normal(size=100)
Y = np.full(100, 3) + X_1 + 2*X_2**2 + e
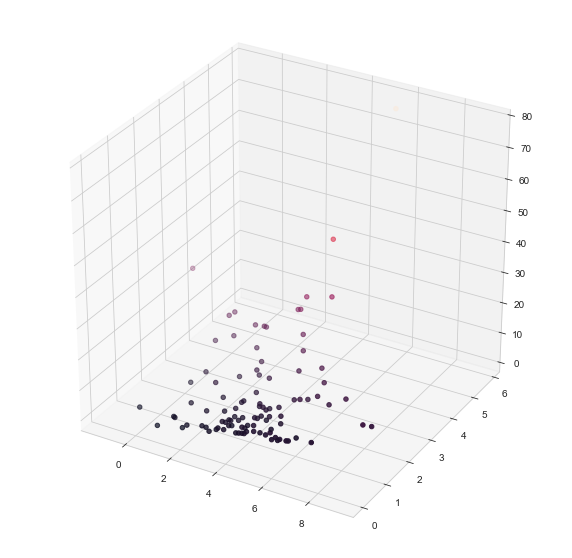
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.scatter3D(X_1, X_2, Y, c=Y)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1a280b4c88>
b. Setting initial value for .
beta_1_hat = 0.2
c. Fitting
from sklearn.linear_model import LinearRegression
A = Y - beta_1_hat*X_1
linreg = LinearRegression()
linreg.fit(X_2.reshape(-1, 1), A)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
normalize=False)
beta_0_hat = linreg.intercept_
f'beta_0_hat = {beta_0_hat}'
'beta_0_hat = 2.8350247328203544'
beta_2_hat = linreg.coef_[0]
f'beta_2_hat = {beta_2_hat}'
'beta_2_hat = 7.512178662654875'
d. Fitting
B = Y - beta_2_hat*X_2
linreg = LinearRegression()
linreg.fit(X_1.reshape(-1, 1), B)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
normalize=False)
beta_0_hat = linreg.intercept_
f'beta_0_hat = {beta_0_hat}'
'beta_0_hat = -0.8300795357307318'
beta_1_hat = linreg.coef_[0]
f'beta_1_hat = {beta_1_hat}'
'beta_1_hat = 1.0727863090555483'
e., f. Backfitting to estimate OLS multiple regression coefficients
def backfit(beta_0_hat, beta_1_hat, beta_2_hat, n_iters=100):
coefs = {'beta_0_hat':[beta_0_hat], 'beta_1_hat':[beta_1_hat], 'beta_2_hat':[beta_2_hat]}
for i in range(n_iters - 1):
# new beta_2_hat
A = Y - beta_1_hat*X_1
linreg = LinearRegression()
linreg.fit(X_2.reshape(-1, 1), A)
beta_2_hat = linreg.coef_[0]
# new beta_0_hat, beta_1_hat
B = Y - beta_2_hat*X_2
linreg = LinearRegression()
linreg.fit(X_1.reshape(-1, 1), B)
beta_0_hat, beta_1_hat = linreg.intercept_, linreg.coef_[0]
# update dict
coefs['beta_0_hat'] += [beta_0_hat]
coefs['beta_1_hat'] += [beta_1_hat]
coefs['beta_2_hat'] += [beta_2_hat]
return coefs
n_iters = 20
backfit_coefs = pd.DataFrame(backfit(beta_0_hat, beta_1_hat, beta_2_hat, n_iters=n_iters))
backfit_coefs.head()
| beta_0_hat | beta_1_hat | beta_2_hat | |
|---|---|---|---|
| 0 | -0.830080 | 1.072786 | 7.512179 |
| 1 | -1.132632 | 1.090675 | 7.717398 |
| 2 | -1.138833 | 1.091042 | 7.721604 |
| 3 | -1.138960 | 1.091049 | 7.721690 |
| 4 | -1.138963 | 1.091050 | 7.721692 |
# get OLS multiple regression coeffs
X = np.stack((X_1, X_2), axis=1)
mreg = LinearRegression()
mreg.fit(X, Y)
mreg_coefs = pd.DataFrame({'beta_0_hat': n_iters*[linreg.intercept_],
'beta_1_hat': n_iters*[linreg.coef_[0]],
'beta_2_hat': n_iters*[linreg.coef_[1]]})
x = np.arange(n_iters)
plt.figure(figsize=(15, 10))
plt.plot(x, backfit_coefs['beta_0_hat'], color='blue')
plt.plot(x, backfit_coefs['beta_1_hat'], color='red')
plt.plot(x, backfit_coefs['beta_2_hat'], color='green')
plt.plot(x, mreg_coefs['beta_0_hat'], color='blue', linestyle='dashed')
plt.plot(x, mreg_coefs['beta_1_hat'], color='red', linestyle='dashed')
plt.plot(x, mreg_coefs['beta_2_hat'], color='green', linestyle='dashed')
plt.legend()
<matplotlib.legend.Legend at 0x1a292b8860>
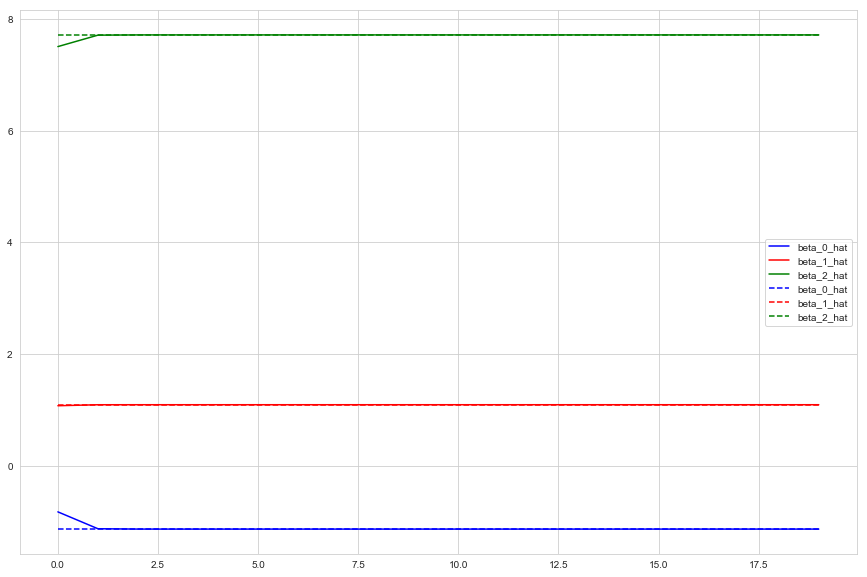
g. How may iterations needed for a good approximation?
# differences of backfit and mreg coefs
backfit_coefs - mreg_coefs
| beta_0_hat | beta_1_hat | beta_2_hat | |
|---|---|---|---|
| 0 | 3.088834e-01 | -1.826322e-02 | -2.095132e-01 |
| 1 | 6.330967e-03 | -3.743286e-04 | -4.294247e-03 |
| 2 | 1.297614e-04 | -7.672352e-06 | -8.801619e-05 |
| 3 | 2.659630e-06 | -1.572549e-07 | -1.804007e-06 |
| 4 | 5.451259e-08 | -3.223144e-09 | -3.697547e-08 |
| 5 | 1.117309e-09 | -6.606249e-11 | -7.578631e-10 |
| 6 | 2.290435e-11 | -1.354250e-12 | -1.553691e-11 |
| 7 | 4.729550e-13 | -2.797762e-14 | -3.206324e-13 |
| 8 | 1.287859e-14 | -4.440892e-16 | -1.065814e-14 |
| 9 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 10 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 11 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 12 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 13 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 14 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 15 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 16 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 17 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 18 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
| 19 | 2.220446e-15 | 0.000000e+00 | -2.664535e-15 |
The differences are all exceedingly small after only a few iterations