islr notes and exercises from An Introduction to Statistical Learning

6. Linear Model Selection and Regularization

Exercise 9: Predicting Apps in College dataset

Preparing the data

import pandas as pd

college = pd.read_csv('../../datasets/College.csv')
college = college.rename({'Unnamed: 0': 'Name'}, axis='columns')
college.head()
Name Private Apps Accept Enroll Top10perc Top25perc F.Undergrad P.Undergrad Outstate Room.Board Books Personal PhD Terminal S.F.Ratio perc.alumni Expend Grad.Rate
0 Abilene Christian University Yes 1660 1232 721 23 52 2885 537 7440 3300 450 2200 70 78 18.1 12 7041 60
1 Adelphi University Yes 2186 1924 512 16 29 2683 1227 12280 6450 750 1500 29 30 12.2 16 10527 56
2 Adrian College Yes 1428 1097 336 22 50 1036 99 11250 3750 400 1165 53 66 12.9 30 8735 54
3 Agnes Scott College Yes 417 349 137 60 89 510 63 12960 5450 450 875 92 97 7.7 37 19016 59
4 Alaska Pacific University Yes 193 146 55 16 44 249 869 7560 4120 800 1500 76 72 11.9 2 10922 15 
college.loc[:, 'Private'] = [0 if entry == 'No' else 1 for entry in college['Private']]
college.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 777 entries, 0 to 776
Data columns (total 19 columns):
Name           777 non-null object
Private        777 non-null int64
Apps           777 non-null int64
Accept         777 non-null int64
Enroll         777 non-null int64
Top10perc      777 non-null int64
Top25perc      777 non-null int64
F.Undergrad    777 non-null int64
P.Undergrad    777 non-null int64
Outstate       777 non-null int64
Room.Board     777 non-null int64
Books          777 non-null int64
Personal       777 non-null int64
PhD            777 non-null int64
Terminal       777 non-null int64
S.F.Ratio      777 non-null float64
perc.alumni    777 non-null int64
Expend         777 non-null int64
Grad.Rate      777 non-null int64
dtypes: float64(1), int64(17), object(1)
memory usage: 115.4+ KB

a. Train - test split

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(college.drop(columns=['Apps', 'Name']), 
                                                    college['Apps'])

b. Linear regression model

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

linreg = LinearRegression().fit(X_train, y_train)

linreg_mse_test = mean_squared_error(y_test, linreg.predict(X_test))
mses_df = pd.DataFrame({'mse_test': linreg_mse_test},
                       index=['linreg'])
mses_df
mse_test
linreg 1.869641e+06

c. Ridge regression model

from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV

parameters = {'alpha': [10**i for i in range(-3, 4)]}
ridge = GridSearchCV(Ridge(), parameters, cv=10, 
                     scoring='neg_mean_squared_error')

%%capture

ridge.fit(X_train, y_train)

%%capture

ridge_cv_df = pd.DataFrame(ridge.cv_results_)
ridge_cv_df

ridge_mse_test = mean_squared_error(y_test, ridge.best_estimator_.predict(X_test))
mses_df = mses_df.append(pd.DataFrame({'mse_test': ridge_mse_test}, index=['ridge']))
mses_df
mse_test
linreg 1.869641e+06
ridge 1.875181e+06

d. Lasso regression model

from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV

parameters = {'alpha': [10**i for i in range(-3, 4)]}
lasso = GridSearchCV(Lasso(), parameters, cv=10, scoring='neg_mean_squared_error')

%%capture

lasso.fit(X_train, y_train)

%%capture

lasso_cv_df = pd.DataFrame(lasso.cv_results_)
lasso_cv_df

lasso_mse_test = mean_squared_error(y_test, lasso.best_estimator_.predict(X_test))
mses_df = mses_df.append(pd.DataFrame({'mse_test': lasso_mse_test}, index=['lasso']))
mses_df
mse_test
linreg 1.869641e+06
ridge 1.875181e+06
lasso 1.870846e+06

e. PCR model

scikit-learn doesn’t have combined PCA and regression so we’ll use the top answer to this CrossValidated question

import numpy as np
from sklearn.preprocessing import scale
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score

n = len(X_train_reduced)
linreg = LinearRegression()

pcr_mses = [-cross_val_score(linreg, np.ones((n,1)), y_train, cv=10, 
                         scoring='neg_mean_squared_error').mean()]   
for i in range(1, college.shape[1] - b1):
    pcr_mses += [-cross_val_score(linreg, X_train_reduced[:, :i], y_train, cv=10, 
                              scoring='neg_mean_squared_error').mean()]

np.argmin(pcr_mses)

17

10 fold Cross-validation selects M=17M = 17 (full PCR model with no intercept).

pcr = LinearRegression().fit(X_train.iloc[:, :np.argmin(pcr_mses)], y_train)

The test error of this model is

pcr_mse_test = mean_squared_error(y_test, pcr.predict(X_test))
mses_df = mses_df.append(pd.DataFrame({'mse_test': pcr_mse_test}, index=['pcr']))
mses_df
mse_test
linreg 1.869641e+06
ridge 1.875181e+06
lasso 1.870846e+06
pcr 1.869641e+06

f. PLS model

from sklearn.cross_decomposition import PLSRegression

# mse for only constant predictor same as for pcr
pls_mses = pcr_mses[:1]

for i in range(1, college.shape[1] - 1):
    pls_mses += [-cross_val_score(estimator=PLSRegression(n_components = i), 
                                  X=X_train, y=y_train, cv=10, 
                                  scoring='neg_mean_squared_error').mean()]

np.argmin(pls_mses)

13

10 fold CV selects M=13M = 13

pls = PLSRegression(n_components=13).fit(X_train, y_train)

pls_mse_test = mean_squared_error(y_test, pls.predict(X_test))
mses_df = mses_df.append(pd.DataFrame({'mse_test': pls_mse_test}, index=['pls']))
mses_df
mse_test
linreg 1.869641e+06
ridge 1.875181e+06
lasso 1.870846e+06
pcr 1.869641e+06
pls 1.862860e+06

g. Comments

How accurately can we predict applications?

The test mses for each model were ≈1.86×106\approx 1.86 \times 10^6. This corresponds to an (absolute) error of 1.86×106≈1387\sqrt{1.86 \times 10^6} \approx 1387 . Given the distribution of applications

college['Apps'].describe()

count      777.000000
mean      3001.638353
std       3870.201484
min         81.000000
25%        776.000000
50%       1558.000000
75%       3624.000000
max      48094.000000
Name: Apps, dtype: float64

import seaborn as sns

% matplotlib inline

sns.distplot(college['Apps'])

<matplotlib.axes._subplots.AxesSubplot at 0x1a212479b0>

png

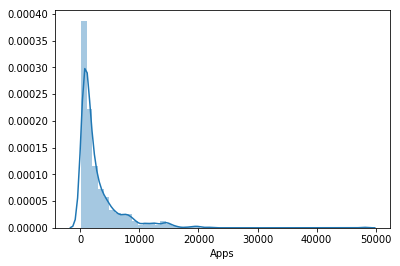
The prediction doesn’t seem that accurate. Given that distribution is highly concentrated about the mean ≈3000\approx 3000 and the upper quartile is ≈3625\approx 3625, we can say that for most values, the prediction is off by ⩾ ≈30%\geqslant\ \approx 30\% of the true value.

Is there much difference among the test errors

No