islr notes and exercises from An Introduction to Statistical Learning

4. Logistic Regression

Exercise 10: Classifying Direction in the Weekly dataset

Preparing the Data

Import

import pandas as pd

weekly = pd.read_csv('../../datasets/Weekly.csv', index_col=0)
weekly.head()
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction
1 1990 0.816 1.572 -3.936 -0.229 -3.484 0.154976 -0.270 Down
2 1990 -0.270 0.816 1.572 -3.936 -0.229 0.148574 -2.576 Down
3 1990 -2.576 -0.270 0.816 1.572 -3.936 0.159837 3.514 Up
4 1990 3.514 -2.576 -0.270 0.816 1.572 0.161630 0.712 Up
5 1990 0.712 3.514 -2.576 -0.270 0.816 0.153728 1.178 Up 
weekly.info()

<class 'pandas.core.frame.DataFrame'>
Int64Index: 1089 entries, 1 to 1089
Data columns (total 9 columns):
Year         1089 non-null int64
Lag1         1089 non-null float64
Lag2         1089 non-null float64
Lag3         1089 non-null float64
Lag4         1089 non-null float64
Lag5         1089 non-null float64
Volume       1089 non-null float64
Today        1089 non-null float64
Direction    1089 non-null object
dtypes: float64(7), int64(1), object(1)
memory usage: 85.1+ KB

Preprocessing

Converting qualitative variables to quantitative

Don’t see any null values but let’s check

weekly.isna().sum().sum()

0

Direction is a qualitative variable encoded as a string; let’s encode it numerically

import sklearn.preprocessing as skl_preprocessing

# create and fit label encoder
direction_le = skl_preprocessing.LabelEncoder()
direction_le.fit(weekly.Direction)

# replace string encoding with numeric
weekly['Direction_num'] = direction_le.transform(weekly.Direction)
weekly.Direction_num.head()

1    0
2    0
3    1
4    1
5    1
Name: Direction_num, dtype: int64

direction_le.classes_

array(['Down', 'Up'], dtype=object)

direction_le.transform(direction_le.classes_)

array([0, 1])

So the encoding is {Down:0, Up:1}

a. Numerical and graphical summaries

Here’s a description of the dataset from the R documentation

Weekly S&P Stock Market Data

Description

Weekly percentage returns for the S&P 500 stock index between 1990 and 2010.

Usage

Weekly
Format

A data frame with 1089 observations on the following 9 variables.

Year
The year that the observation was recorded

Lag1
Percentage return for previous week

Lag2
Percentage return for 2 weeks previous

Lag3
Percentage return for 3 weeks previous

Lag4
Percentage return for 4 weeks previous

Lag5
Percentage return for 5 weeks previous

Volume
Volume of shares traded (average number of daily shares traded in billions)

Today
Percentage return for this week

Direction
A factor with levels Down and Up indicating whether the market had a positive or negative return on a given week

Source

Raw values of the S&P 500 were obtained from Yahoo Finance and then converted to percentages and lagged.

Let’s look at summary statistics

weekly.describe()
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction_num
count 1089.000000 1089.000000 1089.000000 1089.000000 1089.000000 1089.000000 1089.000000 1089.000000 1089.000000
mean 2000.048669 0.150585 0.151079 0.147205 0.145818 0.139893 1.574618 0.149899 0.555556
std 6.033182 2.357013 2.357254 2.360502 2.360279 2.361285 1.686636 2.356927 0.497132
min 1990.000000 -18.195000 -18.195000 -18.195000 -18.195000 -18.195000 0.087465 -18.195000 0.000000
25% 1995.000000 -1.154000 -1.154000 -1.158000 -1.158000 -1.166000 0.332022 -1.154000 0.000000
50% 2000.000000 0.241000 0.241000 0.241000 0.238000 0.234000 1.002680 0.241000 1.000000
75% 2005.000000 1.405000 1.409000 1.409000 1.409000 1.405000 2.053727 1.405000 1.000000
max 2010.000000 12.026000 12.026000 12.026000 12.026000 12.026000 9.328214 12.026000 1.000000

  • All the variables ranges look good (e.g. no negative values for volume)

  • The Lag variables and Today all have very similar summary statistics, as expected.

  • Of particular interest is Direction_num, which has a mean of ≈0.56\approx 0.56 and a standard deviation of ≈0.50\approx 0.50! That’s what we’ll be trying to predict later in the exercise, which will be interesting.

Let’s look at distributions

import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('seaborn-white')
sns.set_style('white')

import warnings  
warnings.filterwarnings('ignore')

import numpy as np

sns.pairplot(weekly, hue='Direction')

<seaborn.axisgrid.PairGrid at 0x1a2515d208>

png

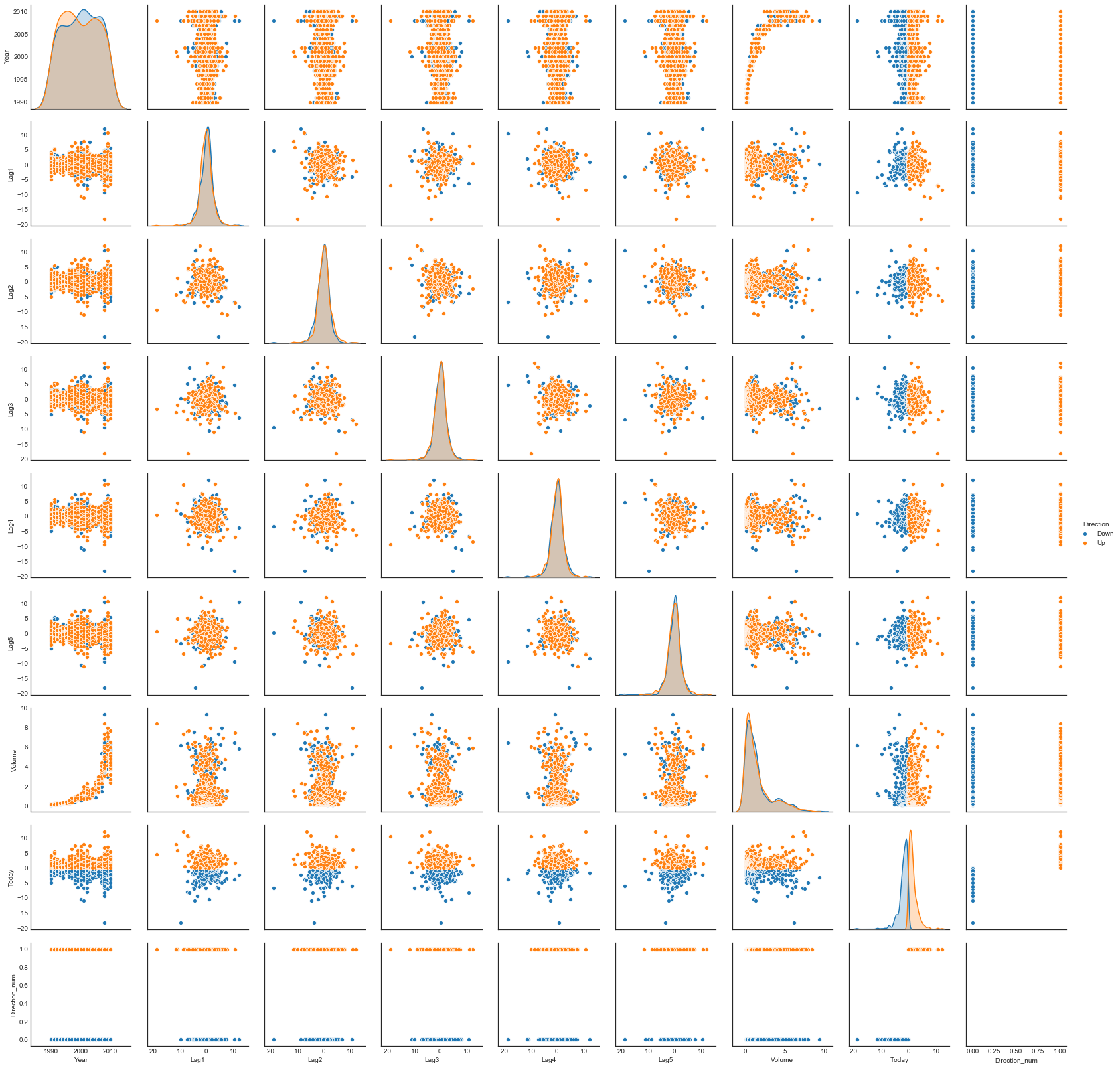
The return variables are concentrated

The return variables (i.e. Lag and Today variables) are “tight” instead of spread out, i.e. fairly concentrated about their mean.

Here are the deviations of all variables as percentages of the magnitude of their ranges

weekly_num = weekly.drop('Direction', axis=1)
round(100 * (weekly_num.std() / (weekly_num.max() - weekly_num.min())), 2)

Year             30.17
Lag1              7.80
Lag2              7.80
Lag3              7.81
Lag4              7.81
Lag5              7.81
Volume           18.25
Today             7.80
Direction_num    49.71
dtype: float64

Return variables are nearly uncorrelated

In the pairplot there is a visible lack of pairwise sample correlation among the return variables.

weekly.corr()
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction_num
Year 1.000000 -0.032289 -0.033390 -0.030006 -0.031128 -0.030519 0.841942 -0.032460 -0.022200
Lag1 -0.032289 1.000000 -0.074853 0.058636 -0.071274 -0.008183 -0.064951 -0.075032 -0.050004
Lag2 -0.033390 -0.074853 1.000000 -0.075721 0.058382 -0.072499 -0.085513 0.059167 0.072696
Lag3 -0.030006 0.058636 -0.075721 1.000000 -0.075396 0.060657 -0.069288 -0.071244 -0.022913
Lag4 -0.031128 -0.071274 0.058382 -0.075396 1.000000 -0.075675 -0.061075 -0.007826 -0.020549
Lag5 -0.030519 -0.008183 -0.072499 0.060657 -0.075675 1.000000 -0.058517 0.011013 -0.018168
Volume 0.841942 -0.064951 -0.085513 -0.069288 -0.061075 -0.058517 1.000000 -0.033078 -0.017995
Today -0.032460 -0.075032 0.059167 -0.071244 -0.007826 0.011013 -0.033078 1.000000 0.720025
Direction_num -0.022200 -0.050004 0.072696 -0.022913 -0.020549 -0.018168 -0.017995 0.720025 1.000000

Indeed the magnitudes of the sample correlations for these pairs are quite small.

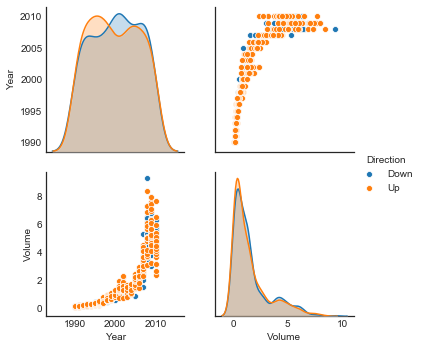
Volume correlates with Year

sns.pairplot(weekly, vars=['Year', 'Volume'], hue='Direction')

<seaborn.axisgrid.PairGrid at 0x1a28503780>

png

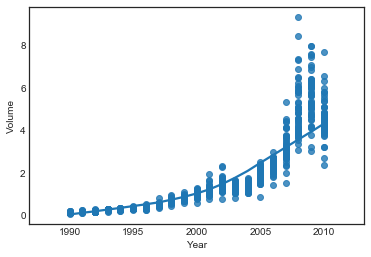
sns.regplot(weekly.Year, weekly.Volume, lowess=True)

<matplotlib.axes._subplots.AxesSubplot at 0x1a2a543be0>

png

b. Logistic Regression Classification of Direction using Lag and Volume predictors

import statsmodels.api as sm

# predictor labels
predictors = ['Lag' + stri. for i in range(1, 6)]
predictors += ['Volume']

# fit and summarize model

sm_logit_model_full = sm.Logit(weekly.Direction_num, sm.add_constant(weekly[predictors]))
sm_logit_model_full.fit().summary()

Optimization terminated successfully.
         Current function value: 0.682441
         Iterations 4
Logit Regression Results
Dep. Variable: Direction_num No. Observations: 1089
Model: Logit Df Residuals: 1082
Method: MLE Df Model: 6
Date: Mon, 26 Nov 2018 Pseudo R-squ.: 0.006580
Time: 17:27:33 Log-Likelihood: -743.18
converged: True LL-Null: -748.10
LLR p-value: 0.1313
coef std err z P>|z| [0.025 0.975]
const 0.2669 0.086 3.106 0.002 0.098 0.435
Lag1 -0.0413 0.026 -1.563 0.118 -0.093 0.010
Lag2 0.0584 0.027 2.175 0.030 0.006 0.111
Lag3 -0.0161 0.027 -0.602 0.547 -0.068 0.036
Lag4 -0.0278 0.026 -1.050 0.294 -0.080 0.024
Lag5 -0.0145 0.026 -0.549 0.583 -0.066 0.037
Volume -0.0227 0.037 -0.616 0.538 -0.095 0.050

Only the intercept and Lag2 and appear to be statistically significant

c. Confusion Matrix

import sklearn.linear_model as skl_linear_model

# fit model
skl_logit_model_full = skl_linear_model.LogisticRegression()
X, Y = sm.add_constant(weekly[predictors]).values, weekly.Direction_num.values
skl_logit_model_full.fit(X, Y)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=None, solver='warn',
          tol=0.0001, verbose=0, warm_start=False)

# check paramaters are close in the two models
abs(skl_logit_model_full.coef_ - sm_logit_model_full.fit().params.values)

Optimization terminated successfully.
         Current function value: 0.682441
         Iterations 4





array([[1.33953314e-01, 6.15092984e-05, 3.94405141e-06, 4.06643634e-05,
        5.96004698e-05, 3.92562567e-05, 3.22507048e-04]])

import sklearn.metrics as skl_metrics

# confusion matrix
confusion_array = skl_metrics.confusion_matrix(Y, skl_logit_model_full.predict(X))
confusion_array

array([[ 54, 430],
       [ 47, 558]])

# confusion data frame
col_index = pd.MultiIndex.from_product([['Pred'], [0, 1]])
row_index = pd.MultiIndex.from_product([['Actual'], [0, 1]])
confusion_df = pd.DataFrame(confusion_array, columns=col_index, index=row_index)
confusion_df.loc[: ,('Pred','Total')] = confusion_df.Pred[0] + confusion_df.Pred[1]
confusion_df.loc[('Actual','Total'), :] = (confusion_df.loc[('Actual',0), :] + 
                                        confusion_df.loc[('Actual',1), :])
confusion_df.astype('int32')
Pred
0 1 Total
Actual 0 54 430 484
1 47 558 605
Total 101 988 1089

Performance rates of interest from the confusion matrix

Recall that for a binary classifier the confusion matrix shows

PredActual(TNFPActNegFNTPActPosPredNegPredPosn) \begin{matrix} \text{Pred} \\ \text{Actual} \begin{pmatrix} TN & FP & ActNeg\\ FN & TP & ActPos\\ PredNeg & PredPos & n \end{pmatrix} \end{matrix}

where

TP=True PositivesFP=False PositivesFN=False NegativesTN=True NegativesActNeg=Total Actual Negatives=TN+FPActPos=Total Actual Positives=FN+TPPredNeg=Total Predicted Negatives=TN+FNPredPos=Total Predicted Positives=FP+TP \begin{aligned} TP & = \text{True Positives}\\ FP & = \text{False Positives}\\ FN & = \text{False Negatives}\\ TN & = \text{True Negatives}\\ ActNeg &= \text{Total Actual Negatives} = TN + FP\\ ActPos &= \text{Total Actual Positives} = FN + TP\\ PredNeg &= \text{Total Predicted Negatives} = TN + FN\\ PredPos &= \text{Total Predicted Positives} = FP + TP\\ \end{aligned}

Also recall the following rates of interest

  • The accuracy of the classifier is the proportion of correctly classified observations

TP+TNn \frac{TP + TN}{n}

i.e., “How often is the model right?”

  • The misclassification rate (or error rate) is the proportion of incorrectly classified observations

FP+FNn \frac{FP + FN}{n}

i.e., “How often is the model wrong?”

  • The null error rate is the proportion of the majority class

max⁡{ActNeg,ActPos}n \frac{\max\{ActNeg, ActPos\}}{n}

i.e. “How often would we be wrong if we always predicted the majority class”

  • The true positive rate (or sensitivity or recall) is the ratio of true positives to actual positives

TPActPos \frac{TP}{ActPos}

, “How often is the model right for actual positives (Y=1Y=1)?”

  • The false positive rate is the ratio of false positives to actual negatives

FPActNeg= \frac{FP}{ActNeg} =

i.e., “How often is the model wrong for actual positives?”

  • The true negative rate or specificity is the ratio of true negatives to actual negatives

TNActNeg \frac{TN}{ActNeg}

i.e., “How often is the model right for actual negatives (Y=0Y=0)?”

  • The false negative rate is the ratio of true negatives to actual negatives

FNActNeg \frac{FN}{ActNeg}

i.e., “How often is the model wrong for actual negatives (Y=0Y=0)?”

  • The precision is the ratio of true positives to predicted positives

TPPredPos \frac{TP}{PredPos}

i.e., “How often are the models’ positive predictions right?”

  • The prevalence is the ratio of actual positives to total observations

FN+TPn \frac{FN + TP}{n}

i.e., “How often do actual positives occur in the sample?”

Analyzing model performance rates

# necessary variables
n = confusion_df.loc[('Actual', 'Total'), ('Pred', 'Total')]
TN = confusion_df.loc[('Actual', 0), ('Pred', 0)]
FP = confusion_df.loc[('Actual', 0), ('Pred', 1)]
FN = confusion_df.loc[('Actual', 1), ('Pred', 0)]
TP = confusion_df.loc[('Actual', 1), ('Pred', 1)]

# compute rates
rates = {}
rates['accuracy'] = (TP + TN) / n
rates['error rate'] = (FP + FN) / n
rates['null error'] = max(FN + TP, FP + TN) / n
rates['TP rate'] = TP / (FN + TP)
rates['FP rate'] = FP / (FN + TP)
rates['TN rate'] = TN / (FP + TN)
rates['FN rate'] = FN / (FP + TN)
rates['precision'] = TP / (FP + TP)
rates['prevalence'] = (FN + TP) / n


# store results
model_perf_rates_df = pd.DataFrame(rates, index=[0])
model_perf_rates_df
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.561983 0.438017 0.555556 0.922314 0.710744 0.11157 0.097107 0.564777 0.555556

Observations

  • The accuracy is ≈56%\approx 56\% so the model is right a bit more than half the time

  • The error rate is ≈44%\approx 44\% so the model is wrong a bit less than half the time

  • The “null error rate” is the error rate of the “null classifier” which always predicts the majority class, which in this case is ≈56%\approx 56\%. Thus our model is about as accurate as the null classifier.

  • The true positive and false positive rates are relatively high. The true negative and false negative rates are relatively low. This makes sense – inspection of the confusion matrix shows that the model predicts positives almost an order of magnitude more often

  • The precision is ≈56%\approx 56\% so the model correctly predicts positives a little more than half the time

  • The prevalence is also ≈56%\approx 56\% so positives occur in the sample a little more than half the time

We’ll package this functionality for later use:

def confusion_results(X, y, skl_model_fit):
    # get confusion array
    confusion_array = skl_metrics.confusion_matrix(y, skl_model_fit.predict(X))

    # necessary variables
    n = np.sum(confusion_array)
    TN = confusion_array[0, 0]
    FP = confusion_array[0, 1]
    FN = confusion_array[1, 0]
    TP = confusion_array[1, 1]

    # compute rates
    rates = {}
    rates['accuracy'] = (TP + TN) / n
    rates['error rate'] = (FP + FN) / n
    rates['null error'] = max(FN + TP, FP + TN) / n
    rates['TP rate'] = TP / (FN + TP)
    rates['FP rate'] = FP / (FN + TP)
    rates['TN rate'] = TN / (FP + TN)
    rates['FN rate'] = FN / (FP + TN)
    rates['precision'] = TP / (FP + TP)
    rates['prevalence'] = (FN + TP) / n


    # return results
    return pd.DataFrame(rates, index=[0])

confusion_results(X, Y, skl_logit_model_full.fit(X, Y))
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.561983 0.438017 0.555556 0.922314 0.710744 0.11157 0.097107 0.564777 0.555556

d. Logistic Regression Classification of Direction using Lag2 predictor

In this section we do some feature selection. Since in b. we found that only Lag2 was a significant feature, we’ll eliminate the others. Further, we’ll train on the years 1990 to 2008 and test on 2009 to 2010

# train/test split
weekly_test, weekly_train = weekly[weekly['Year'] <= 2008], weekly[weekly['Year'] > 2008]
X_train, y_train = sm.add_constant(weekly_train['Lag2']), weekly_train['Direction_num']
X_test, y_test = sm.add_constant(weekly_test['Lag2']), weekly_test['Direction_num']

# fit new model
skl_logit_model_lag2 = skl_linear_model.LogisticRegression()

# confusion matrix
confusion_results(X_test, y_test, skl_logit_model_lag2.fit(X_train, y_train))
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.550254 0.449746 0.552284 0.963235 0.777574 0.040816 0.045351 0.553326 0.552284

The accuracy is actually slightly worse than the full model

e. Other classification models of Direction using Lag2 predictor

LDA

import sklearn.discriminant_analysis as skl_discriminant_analysis

skl_LDA_model_lag2 = skl_discriminant_analysis.LinearDiscriminantAnalysis()

# confusion matrix
confusion_results(X_test, y_test, skl_LDA_model_lag2.fit(X_train, y_train))
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.550254 0.449746 0.552284 0.965074 0.779412 0.038549 0.043084 0.553214 0.552284 
# accuracy
skl_metrics.accuracy_score(y_test, skl_LDA_model_lag2.predict(X_test))

0.550253807106599

Nearly identical to skl_logit_model_lag2!

QDA

skl_QDA_model_lag2 = skl_discriminant_analysis.QuadraticDiscriminantAnalysis()

# confusion matrix
confusion_results(X_test, y_test, skl_QDA_model_lag2.fit(X_train, y_train))
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.447716 0.552284 0.552284 0.0 0.0 1.0 1.23356 NaN 0.552284

Worse accuracy than Logistic Regression and LDA

KNN

import sklearn.neighbors as skl_neighbors

skl_KNN_model_lag2 = skl_neighbors.KNeighborsClassifier(n_neighbors=1)

# confusion matrix
confusion_results(X_test, y_test, skl_KNN_model_lag2.fit(X_train, y_train))
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
0 0.518782 0.481218 0.552284 0.626838 0.498162 0.385488 0.460317 0.55719 0.552284

Comparing results

For neatness and ease of comparison, we’ll package all these results

def confusion_comparison(X, y, models):
    df = pd.concat([confusion_results(X, y, models[model_name]) 
                      for model_name in models])
    df['Model'] = list(models.keys())
    return df.set_index('Model')

models = {'Logit': skl_logit_model_lag2, 'LDA': skl_LDA_model_lag2, 
          'QDA': skl_QDA_model_lag2, 'KNN': skl_KNN_model_lag2}

for model_name in models:
    models[model_name] = models[model_name].fit(X_train, y_train)

conf_comp_df = confusion_comparison(X_test, y_test, models)
conf_comp_df
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
Model
Logit 0.550254 0.449746 0.552284 0.963235 0.777574 0.040816 0.045351 0.553326 0.552284
LDA 0.550254 0.449746 0.552284 0.965074 0.779412 0.038549 0.043084 0.553214 0.552284
QDA 0.447716 0.552284 0.552284 0.000000 0.000000 1.000000 1.233560 NaN 0.552284
KNN 0.518782 0.481218 0.552284 0.626838 0.498162 0.385488 0.460317 0.557190 0.552284

h. Which method has the best results?

As measured by accuracy, Logit and LDA models are tied, with KNN not too far behind and QDA a more distant third.

With respect to other confusion metrics, Logit and LDA are nearly identical

i. Feature and Model Selection

In this section, we’ll experiment to try to find improved performance on the test data. We’ll try:

  • Different subsets of the predictors
  • Interactions among the predictors
  • Transformations of the predictors
  • Different values of KK for KNN

Get all predictor interactions

from itertools import combinations

# all pairs of columns in weekly except year and direction
df = weekly.drop(['Year', 'Direction', 'Direction_num'], axis=1)
col_pairs = combinations(df.columns, 2)

# assemble interactions in dataframe
interaction_df = pd.DataFrame({col1 + ':' + col2: weekly[col1]*weekly[col2] 
                               for (col1, col2) in col_pairs})

# concat data frames
dir_df = weekly[['Direction', 'Direction_num']]
weekly_interact = pd.concat([weekly.drop(['Direction', 'Direction_num'], axis=1),
                             interaction_df, dir_df], axis=1)
weekly_interact.head()
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Lag1:Lag2 Lag1:Lag3 ... Lag3:Volume Lag3:Today Lag4:Lag5 Lag4:Volume Lag4:Today Lag5:Volume Lag5:Today Volume:Today Direction Direction_num
1 1990 0.816 1.572 -3.936 -0.229 -3.484 0.154976 -0.270 1.282752 -3.211776 ... -0.609986 1.062720 0.797836 -0.035490 0.061830 -0.539936 0.940680 -0.041844 Down 0
2 1990 -0.270 0.816 1.572 -3.936 -0.229 0.148574 -2.576 -0.220320 -0.424440 ... 0.233558 -4.049472 0.901344 -0.584787 10.139136 -0.034023 0.589904 -0.382727 Down 0
3 1990 -2.576 -0.270 0.816 1.572 -3.936 0.159837 3.514 0.695520 -2.102016 ... 0.130427 2.867424 -6.187392 0.251265 5.524008 -0.629120 -13.831104 0.561669 Up 1
4 1990 3.514 -2.576 -0.270 0.816 1.572 0.161630 0.712 -9.052064 -0.948780 ... -0.043640 -0.192240 1.282752 0.131890 0.580992 0.254082 1.119264 0.115081 Up 1
5 1990 0.712 3.514 -2.576 -0.270 0.816 0.153728 1.178 2.501968 -1.834112 ... -0.396003 -3.034528 -0.220320 -0.041507 -0.318060 0.125442 0.961248 0.181092 Up 1

5 rows × 31 columns

Choose some transformations

# list of transformations

from numpy import sqrt, sin, log, exp, power

# power functions with odd exponent to preserve sign of inputs
def power_3(array):
    return np.power(array, 3)

def power_5(array):
    return np.power(array, 3)

def power_7(array):
    return np.power(array, 4)

# transformations are functions with domain all real numbers
transforms = [power_3, power_5, power_7, sin, exp]
transforms

[<function __main__.power_3(array)>,
 <function __main__.power_5(array)>,
 <function __main__.power_7(array)>,
 <ufunc 'sin'>,
 <ufunc 'exp'>]

Random data tweak

We’ll write a simple function which returns a dataset which has

  • as predictors a random subset of the predictors and interactions of the original dataset (i.e. a random subset of the columns of weekly_interact)
  • a random subset of its predictors transformed by a random choice of transformations from transform

We call such a dataset a “random data tweak”

import numpy as np

def random_data_tweak(weekly_interact, transforms):
    # drop undersirable columns
    weekly_drop = weekly_interact.drop(['Year', 'Direction', 'Direction_num'], axis=1)

    # choose a random subset of the predictors
    predictor_labels = np.random.choice(weekly_drop.columns, 
                                  size=np.random.randint(1, high=weekly_drop.shape[1] + 1),
                                  replace=False)


    # choose a random subset of these to transform
    trans_predictor_labels = np.random.choice(predictor_labels, 
                                          size=np.random.randint(0, len(predictor_labels)),
                                          replace=False)

    # choose random transforms
    some_transforms = np.random.choice(transforms,
                                  size=len(trans_predictor_labels),
                                  replace=True)

    # create the df
    df = weekly_interact[predictor_labels].copy()

    # transform appropriate columns
    for i in range(0, len(trans_predictor_labels)):
        # do transformation
        df.loc[ : , trans_predictor_labels[i]] = some_transforms[i](df[trans_predictor_labels[i]])
        # rename to reflect which transformation was used
        df = df.rename({trans_predictor_labels[i]: 
                    some_transforms[i].__name__ + '(' + trans_predictor_labels[i] + ')' }, axis='columns')

    return pd.concat([df, weekly_interact['Direction_num']], axis=1)

random_data_tweak(weekly_interact, transforms).head()
Lag3-Lag5 power_7(Volume-Today) power_5(Lag5) Lag2-Lag5 power_3(Lag4-Lag5) sin(Lag4) Lag2-Today exp(Lag1-Lag5) Lag1 power_5(Lag4-Volume) exp(Lag1-Today) Lag4-Today sin(Lag5-Volume) Lag3-Today power_3(Lag3-Lag4) exp(Lag2) Direction_num
1 13.713024 0.000003 -42.289684 -5.476848 0.507856 -0.227004 -0.424440 0.058254 0.816 -0.000045 0.802262 0.061830 -0.514081 1.062720 0.732271 4.816271 0
2 -0.359988 0.021456 -0.012009 -0.186864 0.732271 0.713448 -2.102016 1.063781 -0.270 -0.199983 2.004751 10.139136 -0.034017 -4.049472 -236.877000 2.261436 0
3 -3.211776 0.099523 -60.976890 1.062720 -236.877000 0.999999 -0.948780 25314.585232 -2.576 0.015863 0.000117 5.524008 -0.588434 2.867424 2.110708 0.763379 1
4 -0.424440 0.000175 3.884701 -4.049472 2.110708 0.728411 -1.834112 250.637582 3.514 0.002294 12.206493 0.580992 0.251357 -0.192240 -0.010695 0.076078 1
5 -2.102016 0.001075 0.543338 2.867424 -0.010695 -0.266731 4.139492 1.787811 0.712 -0.000072 2.313441 -0.318060 0.125113 -3.034528 0.336456 33.582329 1

Comparison of Logit, LDA, QDA, and KNN models on a single random data tweak

import sklearn.model_selection as skl_model_selection

def model_comparison():
    # tweak data
    tweak_df = random_data_tweak(weekly_interact, transforms)
    
    # train test split
    X, y = sm.add_constant(tweak_df.drop(['Direction_num'], axis=1).values), tweak_df['Direction_num'].values
    X_train, X_test, y_train, y_test = skl_model_selection.train_test_split(X, y)
    
    # dict for models
    models = {}

    # train param models
    models['Logit'] = skl_linear_model.LogisticRegression(solver='lbfgs').fit(X_train, y_train)
    models['LDA'] = skl_discriminant_analysis.LinearDiscriminantAnalysis().fit(X_train, y_train)
    models['QDA'] =  skl_discriminant_analysis.QuadraticDiscriminantAnalysis().fit(X_train, y_train)
    
    # train KNN models for K = 1,..,5
    for i in range(1, 6):
        models['KNN' + stri.] = skl_neighbors.KNeighborsClassifier(n_neighbors=i).fit(X_train, y_train)
    
    
    return {'predictors': tweak_df.columns, 'comparison': confusion_comparison(X_test, y_test, models)}    

model_comparison()

Comparison of Logit, LDA, QDA, and KNN models over nn data tweaks

def model_comparisons(n):
    # running list of predictors and dfs from each comparison
    predictors_list = []
    dfs = []
    
    # iterate comparisons
    for i in range(n):
        # get comparison result
        result = model_comparison()
        predictors_list += [result['predictors']]
        
        # set MultiIndex
        df = result['comparison']
        df['Instance'] = i
        df = df.reset_index()
        df  = df.set_index(['Instance', 'Model'])
        
        # add results to running lists
        dfs += [df]
    
    return {'predictors': predictors_list, 'comparisons': pd.concat(dfs)}

results = model_comparisons(1000)

Here are the first 3 comparisons:

comparisons_df = results['comparisons']
comparisons_df.head(21)
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
Instance Model
0 Logit 0.560440 0.439560 0.549451 0.666667 0.466667 0.430894 0.406504 0.588235 0.549451
LDA 0.948718 0.051282 0.549451 1.000000 0.093333 0.886179 0.000000 0.914634 0.549451
QDA 0.450549 0.549451 0.549451 0.000000 0.000000 1.000000 1.219512 NaN 0.549451
KNN1 0.714286 0.285714 0.549451 0.760000 0.280000 0.658537 0.292683 0.730769 0.549451
KNN2 0.688645 0.311355 0.549451 0.553333 0.120000 0.853659 0.544715 0.821782 0.549451
KNN3 0.703297 0.296703 0.549451 0.740000 0.280000 0.658537 0.317073 0.725490 0.549451
KNN4 0.699634 0.300366 0.549451 0.653333 0.200000 0.756098 0.422764 0.765625 0.549451
KNN5 0.703297 0.296703 0.549451 0.760000 0.300000 0.634146 0.292683 0.716981 0.549451
1 Logit 0.937729 0.062271 0.523810 0.979021 0.097902 0.892308 0.023077 0.909091 0.523810
LDA 0.695971 0.304029 0.523810 0.965035 0.545455 0.400000 0.038462 0.638889 0.523810
QDA 0.476190 0.523810 0.523810 0.000000 0.000000 1.000000 1.100000 NaN 0.523810
KNN1 0.706960 0.293040 0.523810 0.769231 0.328671 0.638462 0.253846 0.700637 0.523810
KNN2 0.710623 0.289377 0.523810 0.587413 0.139860 0.846154 0.453846 0.807692 0.523810
KNN3 0.706960 0.293040 0.523810 0.790210 0.349650 0.615385 0.230769 0.693252 0.523810
KNN4 0.695971 0.304029 0.523810 0.650350 0.230769 0.746154 0.384615 0.738095 0.523810
KNN5 0.725275 0.274725 0.523810 0.825175 0.349650 0.615385 0.192308 0.702381 0.523810
2 Logit 0.454212 0.545788 0.545788 0.000000 0.000000 1.000000 1.201613 NaN 0.545788
LDA 0.967033 0.032967 0.545788 0.959732 0.020134 0.975806 0.048387 0.979452 0.545788
QDA 0.454212 0.545788 0.545788 0.000000 0.000000 1.000000 1.201613 NaN 0.545788
KNN1 0.501832 0.498168 0.545788 0.510067 0.422819 0.491935 0.588710 0.546763 0.545788
KNN2 0.487179 0.512821 0.545788 0.308725 0.248322 0.701613 0.830645 0.554217 0.545788

Here are the predictors used for the first 3 comparisons:

predictors_list = results['predictors']

predictors_list[0:3]

[Index(['Lag2-Today', 'Lag4-Volume', 'Lag2-Lag3', 'Volume-Today', 'Lag2',
        'power_7(Lag1-Volume)', 'Lag1-Lag2', 'Lag2-Volume', 'Lag4-Today',
        'sin(Lag3-Today)', 'Lag3-Lag4', 'Lag5-Volume', 'Today',
        'power_5(Lag3-Lag5)', 'Lag1-Lag5', 'Lag4', 'Direction_num'],
       dtype='object'),
 Index(['Lag3-Lag5', 'Lag5-Today', 'Lag1', 'sin(Lag2-Volume)', 'Lag2-Today',
        'power_5(Volume)', 'Lag4-Lag5', 'Lag1-Lag2', 'power_5(Lag2-Lag3)',
        'Lag3-Today', 'Lag3-Volume', 'Volume-Today', 'Lag1-Today',
        'Direction_num'],
       dtype='object'),
 Index(['power_3(Lag2-Lag3)', 'Lag1-Today', 'Lag4-Volume', 'sin(Lag1-Lag2)',
        'power_7(Lag2-Today)', 'Lag1', 'exp(Lag2-Lag4)', 'power_3(Volume)',
        'exp(Lag3-Lag5)', 'exp(Lag5)', 'power_5(Lag1-Lag5)', 'Today',
        'Lag1-Lag3', 'Lag4-Today', 'power_5(Lag5-Today)', 'exp(Lag3-Lag4)',
        'power_7(Lag3-Today)', 'sin(Lag2)', 'sin(Volume-Today)',
        'power_3(Lag2-Volume)', 'Lag1-Lag4', 'power_7(Lag4-Lag5)',
        'exp(Lag5-Volume)', 'Direction_num'],
       dtype='object')]

Analysis of Comparisons

Analyzing accuracy across models

Summary statistics
grouped_by_model = comparisons_df.groupby(level=1)
grouped_by_model.mean()
accuracy error rate null error TP rate FP rate TN rate FN rate precision prevalence
Model
KNN1 0.626147 0.373853 0.556381 0.668314 0.342757 0.574424 0.418527 0.662625 0.55615
KNN2 0.601912 0.398088 0.556381 0.463810 0.180901 0.775631 0.676137 0.707457 0.55615
KNN3 0.629945 0.370055 0.556381 0.690867 0.358510 0.555069 0.390503 0.661137 0.55615
KNN4 0.615769 0.384231 0.556381 0.544830 0.237261 0.705825 0.574505 0.691635 0.55615
KNN5 0.631011 0.368989 0.556381 0.706117 0.371881 0.538619 0.371593 0.658446 0.55615
LDA 0.726355 0.273645 0.556381 0.942929 0.437290 0.456703 0.073307 0.717898 0.55615
Logit 0.551216 0.448784 0.556381 0.368049 0.176416 0.782584 0.797881 0.697051 0.55615
QDA 0.462040 0.537960 0.556381 0.085262 0.053065 0.933012 1.151742 0.619088 0.55615 
grouped_by_model.mean().accuracy.sort_values(ascending=False)

Model
LDA      0.726355
KNN5     0.631011
KNN3     0.629945
KNN1     0.626147
KNN4     0.615769
KNN2     0.601912
Logit    0.551216
QDA      0.462040
Name: accuracy, dtype: float64

Let’s look at summary statistics for accuracy

grouped_by_model.accuracy.describe()
count mean std min 25% 50% 75% max
Model
KNN1 1000.0 0.626147 0.111154 0.435897 0.545788 0.600733 0.684982 1.000000
KNN2 1000.0 0.601912 0.112694 0.421245 0.516484 0.578755 0.659341 1.000000
KNN3 1000.0 0.629945 0.110973 0.443223 0.549451 0.604396 0.682234 1.000000
KNN4 1000.0 0.615769 0.113840 0.410256 0.531136 0.589744 0.670330 0.996337
KNN5 1000.0 0.631011 0.112222 0.439560 0.549451 0.600733 0.692308 1.000000
LDA 1000.0 0.726355 0.177813 0.476190 0.556777 0.699634 0.941392 0.996337
Logit 1000.0 0.551216 0.186576 0.369963 0.439560 0.468864 0.553114 1.000000
QDA 1000.0 0.462040 0.072413 0.369963 0.428571 0.446886 0.468864 0.967033

Interesting – all models were able to get very close to or achieve 100% accuracy at least once.

TO DO: Try to find similarities in predictors/transformations for the instances which gave maximum classification accuracy

Let’s look at some distributions.

Distributions of accuracy across models
Parametric models
import seaborn as sns
sns.set_style('white')

param_models = ['Logit', 'LDA', 'QDA']

for model_name in param_models:
    sns.distplot(grouped_by_model.accuracy.get_group(model_name), label=model_name)

plt.legend()

<matplotlib.legend.Legend at 0x1a254db860>

png

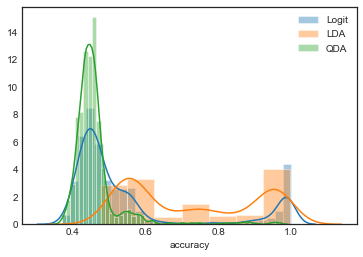
Observations

  • There are some interesting peaks here – the distributions look bimodal.
  • Both Logit and QDA models are highly concentrated in low accuracy, but LDA is more spread out

TO DO: Try to find similarities in predictors/transformations for the instances clustered around these two modes

KNN models
sns.distplot(grouped_by_model.accuracy.get_group('KNN1'), label='KNN1')

plt.legend()

<matplotlib.legend.Legend at 0x1a252924a8>

png

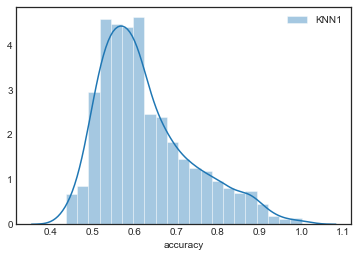
sns.distplot(grouped_by_model.accuracy.get_group('KNN2'), label='KNN2')

<matplotlib.axes._subplots.AxesSubplot at 0x1a2a6e6940>

png

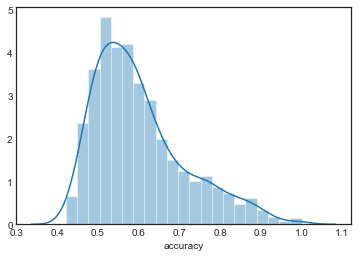
sns.distplot(grouped_by_model.accuracy.get_group('KNN3'), label='KNN3')

<matplotlib.axes._subplots.AxesSubplot at 0x1a25ce2cc0>

png

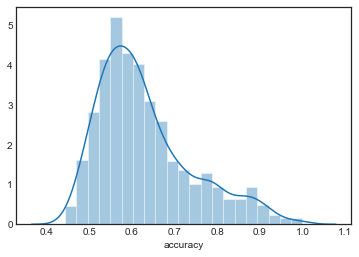
sns.distplot(grouped_by_model.accuracy.get_group('KNN4'), label='KNN4')

<matplotlib.axes._subplots.AxesSubplot at 0x1a2569ad30>

png

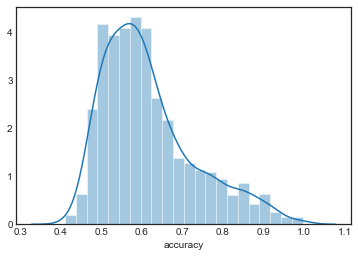
sns.distplot(grouped_by_model.accuracy.get_group('KNN5'), label='KNN5')

<matplotlib.axes._subplots.AxesSubplot at 0x1a25ca3dd8>

png

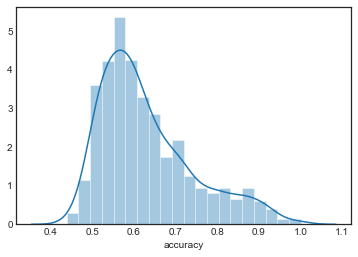
The distributions are all very similar, although they appear to become more concentrated as NN increases.