islr notes and exercises from An Introduction to Statistical Learning

3. Linear Regression

Exercise 13: Regression models on simulated data

a. Generate feature data

import numpy as np

np.random.seed(0)
x = np.random.normal(loc=0, scale=1, size=100)

b. Generate noise

eps = np.random.normal(loc=0, scale=0.25, size=100)

c. Generate response data

y = -1 + 0.5*x + eps

y.shape

(100,)

In this case, β0=−1,β1=0.5\beta_0 = -1, \beta_1 = 0.5.

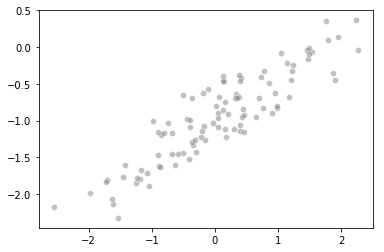
d. Scatterplot

%matplotlib inline
import seaborn as sns

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)

<matplotlib.axes._subplots.AxesSubplot at 0x1a201c7a58>

png

e. Fitting a least squares regression model

from sklearn.linear_model import LinearRegression

linear_model = LinearRegression().fit(x.reshape(-1, 1), y)

We find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(linear_model.intercept_, 4), round(linear_model.coef_[0], 4))

(-0.9812, 0.5287)

Not too far from the true value of (-1, 0.5)

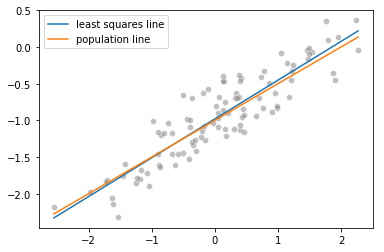
f. Plotting the least squares and population lines

import matplotlib.pyplot as plt

%matplotlib inline

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)
sns.lineplot(x, linear_model.predict(x.reshape(-1, 1)), label="least squares line")
sns.lineplot(x, -1 + 0.5*x, label="population line")

plt.legend()

<matplotlib.legend.Legend at 0x1a2019b550>

png

g. Fitting a least squares quadratic regression model

import pandas as pd

data_1 = pd.DataFrame({'x': x, 'x_sq': x**2, 'y': y})

quadratic_model = LinearRegression().fit(data_1[['x', 'x_sq']].values, data_1['y'].values)

In this case we find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(quadratic_model.intercept_, 4), round(quadratic_model.coef_[0], 4))

(-0.9643, 0.5308)

The difference between the two models is

(round(abs(linear_model.intercept_ - quadratic_model.intercept_), 4), 
 round(abs(linear_model.coef_[0] - quadratic_model.coef_[0]), 4))

(0.0169, 0.0021)

Still very close to the true value of (-1, 0.5), but not as close as the linear model. This at least is is not evidence that the quadratic term improves the fit

h. Repeating a. - f. with less noise

Generate feature data
import numpy as np

np.random.seed(0)
x = np.random.normal(loc=0, scale=1, size=100)
Generate noise with order of magnitude less variance
eps = np.random.normal(loc=0, scale=0.025, size=100)
Generate response data
y = -1 + 0.5*x + eps

y.shape

(100,)
Scatterplot
import seaborn as sns

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)

<matplotlib.axes._subplots.AxesSubplot at 0x1a20fadeb8>

png

Fitting a least squares regression model
from sklearn.linear_model import LinearRegression

linear_model = LinearRegression().fit(x.reshape(-1, 1), y)

We find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(linear_model.intercept_, 4), round(linear_model.coef_[0], 4))

(-0.9981, 0.5029)

This is very close to the true value of (-1, 0.5)

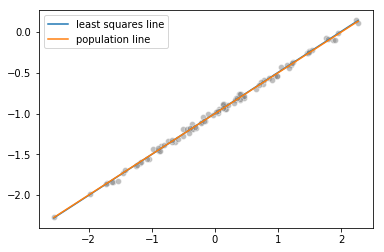
Plotting the least squares and population lines
import matplotlib.pyplot as plt

%matplotlib inline

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)
sns.lineplot(x, linear_model.predict(x.reshape(-1, 1)), label="least squares line")
sns.lineplot(x, -1 + 0.5*x, label="population line")

plt.legend()

<matplotlib.legend.Legend at 0x1a20f06240>

png

Fitting a least squares quadratic regression model
import pandas as pd

data_2 = pd.DataFrame({'x': x, 'x_sq': x**2, 'y': y})

quadratic_model = LinearRegression().fit(data_2[['x', 'x_sq']].values, data_2['y'].values)

In this case we find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(quadratic_model.intercept_, 4), round(quadratic_model.coef_[0], 4))

(-0.9964, 0.5031)

Still very close to the true value of (-1, 0.5), but not as close as the linear model.The difference between the two models is

(round(abs(linear_model.intercept_ - quadratic_model.intercept_), 4), 
 round(abs(linear_model.coef_[0] - quadratic_model.coef_[0]), 4))

(0.0017, 0.0002)

However the difference between the two models is smaller now

i. Repeating a. - f. with more noise

Generate feature data
import numpy as np

np.random.seed(0)
x = np.random.normal(loc=0, scale=1, size=100)
Generate noise with order of magnitude more variance
eps = np.random.normal(loc=0, scale=2.5, size=100)
Generate response data
y = -1 + 0.5*x + eps

y.shape

(100,)
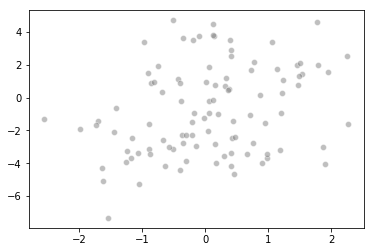
Scatterplot
import seaborn as sns

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)

<matplotlib.axes._subplots.AxesSubplot at 0x1a2114fbe0>

png

Fitting a least squares regression model
from sklearn.linear_model import LinearRegression

linear_model = LinearRegression().fit(x.reshape(-1, 1), y)

We find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(linear_model.intercept_, 4), round(linear_model.coef_[0], 4))

(-0.8121, 0.7867)

Much farther from the true value of (-1, 0.5) in previous cases

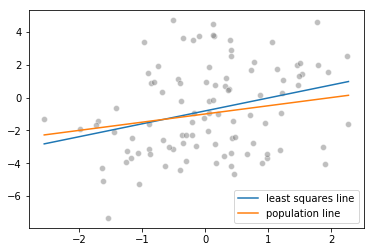
Plotting the least squares and population lines
import matplotlib.pyplot as plt

%matplotlib inline

sns.scatterplot(x, y, facecolors='grey', edgecolors='grey', alpha=0.5)
sns.lineplot(x, linear_model.predict(x.reshape(-1, 1)), label="least squares line")
sns.lineplot(x, -1 + 0.5*x, label="population line")

plt.legend()

<matplotlib.legend.Legend at 0x1a21073748>

png

Fitting a least squares quadratic regression model
import pandas as pd

data_3 = pd.DataFrame({'x': x, 'x_sq': x**2, 'y': y})

quadratic_model = LinearRegression().fit(data_3[['x', 'x_sq']].values, data_3['y'].values)

In this case we find β^=(β^0,β^1)\hat{\beta}=(\hat{\beta}_0, \hat{\beta}_1) is

(round(quadratic_model.intercept_, 4), round(quadratic_model.coef_[0], 4))

(-0.6432, 0.8076)

Even further from the true value than the linear model

(round(abs(linear_model.intercept_ - quadratic_model.intercept_), 4), 
 round(abs(linear_model.coef_[0] - quadratic_model.coef_[0]), 4))

(0.1689, 0.0208)

The difference between the two models is greater than the previous cases

j. Confidence intervals for the coefficients

import statsmodels.formula.api as smf

linear_model_1 = smf.ols('y ~ x', data=data_1).fit()
linear_model_2 = smf.ols('y ~ x', data=data_2).fit()
linear_model_3 = smf.ols('y ~ x', data=data_3).fit()

linear_model_1.conf_int()
0 1
Intercept -1.03283 -0.929593
x 0.47755 0.579800 
linear_model_2.conf_int()
0 1
Intercept -1.003283 -0.992959
x 0.497755 0.507980 
linear_model_3.conf_int()
0 1
Intercept -1.328304 -0.295930
x 0.275495 1.297997