3. Linear Regression

Exercise 8: Simple regression of `mpg` on `horsepower` in `auto` dataset

Preparing the dataset
a. Fitting the model
b. Scatterplot and least squares line plot
c. Diagnostic plots
Footnotes

Preparing the dataset

Import pandas, load the Auto dataset, and inspect

import pandas as pd

auto = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Auto.csv')
auto.head()

	mpg	cylinders	displacement	horsepower	weight	acceleration	year	origin	name
0	18.0	8	307.0	130	3504	12.0	70	1	chevrolet chevelle malibu
1	15.0	8	350.0	165	3693	11.5	70	1	buick skylark 320
2	18.0	8	318.0	150	3436	11.0	70	1	plymouth satellite
3	16.0	8	304.0	150	3433	12.0	70	1	amc rebel sst
4	17.0	8	302.0	140	3449	10.5	70	1	ford torino

auto.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 397 entries, 0 to 396
Data columns (total 9 columns):
mpg             397 non-null float64
cylinders       397 non-null int64
displacement    397 non-null float64
horsepower      397 non-null object
weight          397 non-null int64
acceleration    397 non-null float64
year            397 non-null int64
origin          397 non-null int64
name            397 non-null object
dtypes: float64(3), int64(4), object(2)
memory usage: 28.0+ KB

All the dtypes look good except horsepower.

auto.horsepower = pd.to_numeric(auto.horsepower, errors='coerce')
auto.horsepower.dtype

dtype('float64')

a. Fitting the model

There are lots of way to do simple linear regression with Python. For statistical analysis, statsmodel is useful.

import statsmodels.api as sm

# filter out null entries
X = auto.horsepower[auto.mpg.notna() & auto.horsepower.notna()]
Y = auto.mpg[auto.mpg.notna() & auto.horsepower.notna()]
X

# add constant
X = sm.add_constant(X)

# create and fit model
model = sm.OLS(Y, X)
model = model.fit()

# show results summary
model.summary()

OLS Regression Results
Dep. Variable:	mpg	R-squared:	0.606
Model:	OLS	Adj. R-squared:	0.605
Method:	Least Squares	F-statistic:	599.7
Date:	Sat, 27 Oct 2018	Prob (F-statistic):	7.03e-81
Time:	08:23:54	Log-Likelihood:	-1178.7
No. Observations:	392	AIC:	2361.
Df Residuals:	390	BIC:	2369.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
const	39.9359	0.717	55.660	0.000	38.525	41.347
horsepower	-0.1578	0.006	-24.489	0.000	-0.171	-0.145

Omnibus:	16.432	Durbin-Watson:	0.920
Prob(Omnibus):	0.000	Jarque-Bera (JB):	17.305
Skew:	0.492	Prob(JB):	0.000175
Kurtosis:	3.299	Cond. No.	322.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Now to answer the questions

i. Is there a relationship between `horsepower` and `mpg`?

This question is answered by testing the hypothesis

$H_0: \beta_1 = 0$ $H_a: \beta_1 \neq 0$

In the results summary table above, the value P>|t| in the row horsepower is the p-value for our hypothesis test. Since it’s $< 0.5e-3$ , we reject $H_0$ and conclude there is a relationship between mpg and hp

ii. How strong is the relationship?

This question is answered by checking the $R^2$ value.

model.rsquared

0.6059482578894348

It’s hard to interpret this based on the current state of my knowledge about the data. Interpretation is discussed on page 70 of the book, but it’s not clear where this problem fits into that discussion.

Given $\min(R^2) = 0$ indicates no relationship and $\max(R^2) = 1$ indicates a perfect (linear) relationship, I’ll say this is a somewhat strong relationship.

iii. Is the relationship positive or negative?

This is given by the sign of $\beta_1$

model.params

const         39.935861
horsepower    -0.157845
dtype: float64

Since $\beta_1 = -0.157845$ , the relationship is negative

iv. What is the predicted `mpg` associated with a `horsepower` of 98? What are the associated 95/ confidence and prediction intervals?

prediction = model.get_prediction([1, 98])
pred_df = prediction.summary_frame()
pred_df.head()

	mean	mean_se	mean_ci_lower	mean_ci_upper	obs_ci_lower	obs_ci_upper
0	24.467077	0.251262	23.973079	24.961075	14.809396	34.124758

The predicted value for mpg=98 is

pred_df['mean']

0    24.467077
Name: mean, dtype: float64

The confidence interval is

(pred_df['mean_ci_lower'].values[0], pred_df['mean_ci_upper'].values[0])

(23.97307896070394, 24.961075344320907)

While the prediction interval is

(pred_df['obs_ci_lower'].values[0], pred_df['obs_ci_upper'].values[0])

(14.809396070967116, 34.12475823405773)

b. Scatterplot and least squares line plot

# setup
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

%matplotlib inline
plt.style.use('seaborn-white')
sns.set_style('white')

For convenience, assemble the results in a new dataframe

# get full prediction results
pred_df = model.get_prediction().summary_frame()

# rename columns to avoid `mean` name conflicts and other confusions
new_names = {}
for name in pred_df.columns:
    if 'mean' in name:
        new_names[name] = name.replace('mean', 'mpg_pred')
    elif 'obs_ci' in name:
        new_names[name] = name.replace('obs_ci', 'mpg_pred_pi')
    else:
        new_names[name] = name
pred_df = pred_df.rename(new_names, axis='columns')

# concat mpg, horsepower and prediction results in dataframe
model_df = pd.concat([X, Y, pred_df], axis=1)
model_df.head()

	const	horsepower	mpg	mpg_pred	mpg_pred_se	mpg_pred_ci_lower	mpg_pred_ci_upper	mpg_pred_pi_lower	mpg_pred_pi_upper
0	1.0	130.0	18.0	19.416046	0.297444	18.831250	20.000841	9.753295	29.078797
1	1.0	165.0	15.0	13.891480	0.462181	12.982802	14.800158	4.203732	23.579228
2	1.0	150.0	18.0	16.259151	0.384080	15.504025	17.014277	6.584598	25.933704
3	1.0	150.0	16.0	16.259151	0.384080	15.504025	17.014277	6.584598	25.933704
4	1.0	140.0	17.0	17.837598	0.337403	17.174242	18.500955	8.169775	27.505422

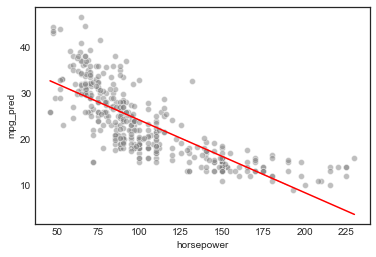
# plot
sns.scatterplot(model_df.horsepower, model_df.mpg, facecolors='grey', alpha=0.5)
sns.lineplot(model_df.horsepower, model_df.mpg_pred, color='r')

png

c. Diagnostic plots

This exercise uses R’s plot() function, which by default returns four diagnostic plots. We’ll recreate those plots in python ¹

Studentized Residuals vs. Fitted plot

This helps identify non-linearity

# add studentized residuals to the dataframe
model_df['resid'] = model.resid

# studentized residuals vs. predicted values plot
sns.regplot(model_df.mpg_pred, model_df.resid/model_df.resid.std(), lowess=True, 
            line_kws={'color':'r', 'lw':1},
            scatter_kws={'facecolors':'grey', 'edgecolors':'grey', 'alpha':0.4})
plt.ylabel('studentized resid')

Text(0,0.5,'studentized resid')

png

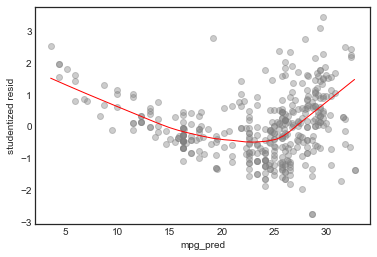
This is a pretty clear indication of non-linearity (see p93) of text). We can also see some outliers

QQ-plot of Residuals

This tests the assumption that the errors are normally distributed

# plot standardized residuals against a standard normal distribution
sm.qqplot(model_df.resid/model_df.resid.std(), color='grey', alpha=0.5, xlabel='')
plt.ylabel('studentized resid quantiles')
plt.xlabel('standard normal quantiles')

png

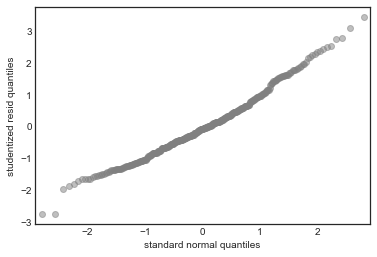
In this case there’s good agreement with the normality assumption

Scale-location plot

This tests the assumption of homoscedasticity (equal variance) of the errors

sns.regplot(model_df.mpg_pred, np.sqrt(np.abs(model_df.resid/model_df.resid.std())), lowess=True, 
            line_kws={'color':'r', 'lw':1},
            scatter_kws={'facecolors':'grey', 'edgecolors':'grey', 'alpha':0.4})
plt.ylabel('√|studentized resid|')

png

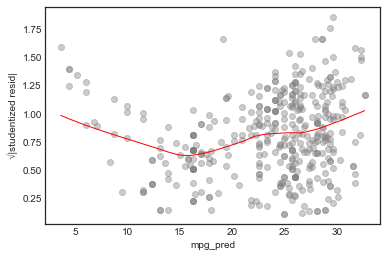
In this case, the assumptions seems unjustified.

Influence Plot

This helps identify influence points, i.e. points with an “outsize” effect on the model ²

# scatterplot of leverage vs studentized residuals
axes = sns.regplot(model.get_influence().hat_matrix_diag, model_df.resid/model_df.resid.std(), 
            lowess=True, 
            line_kws={'color':'r', 'lw':1},
            scatter_kws={'facecolors':'grey', 'edgecolors':'grey', 'alpha':0.4})
plt.xlabel('leverage')
plt.ylabel('studentized resid')

# plot Cook's distance contours for D = 0.5, D = 1
x = np.linspace(axes.get_xlim()[0], axes.get_xlim()[1], 50)
plt.plot(x, np.sqrt(0.5*(1 - x)/x), color='red', linestyle='dashed')
plt.plot(x, np.sqrt((1 - x)/x), color='red', linestyle='dashed')

png

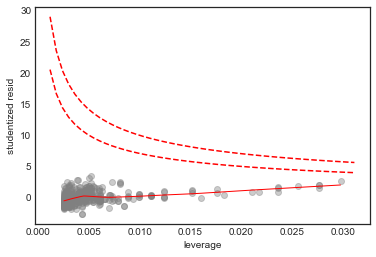
No point in this plot has both high leverage and high residual, and all the points in this plot are within the Cook’s distance contours, so we conclude that there are no high influence points

Footnotes

This Medium article addresses the same issue. ↩
This Cross-Validated question was helpful in figuring out how to plot the Cook’s distance. ↩

islr notes and exercises from An Introduction to Statistical Learning